В непозиционных системах счисления смысл каждой цифры не зависит от ее расположения в числе. Недостатком таких систем является сложность записи чисел и отсутствие стандартных формальных правил арифметических действий над ними. В связи с этим такая система сейчас используется редко.
Например, в римской системе используются цифры
с помощью которых можно записать любое число, например
Число – это знак, обозначающий определенное количество чего-либо. Такие знаки записываются на основании правил, которые составляют так называемую систему счисления. Числа в любой системе счисления записываются с помощью специальных отличных друг от друга знаков, которые называются цифрами. Существуют различные системы счисления, они делятся на два класса – непозиционные и позиционные. Привычная нам десятичная система – позиционная.
В позиционных системах счисления смысл цифры зависит от места ее расположения в числе, а запись чисел и правила выполнения арифметических действий с ними стандартизованы и формализованы. В такой системе счисления число – это краткая запись суммы.
Например, в десятичной, когда мы пишем число 168, мы подразумеваем, что в этом числе 8 единиц, 6 десятков и 1 сотня. То есть
То есть число – это последовательность коэффициентов при степенях числа 10. Другими словами, если имеем число
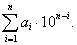
Позиционная система счисления задается величиной основания и множеством цифр. Наименьшая цифра – нуль, каждая следующая цифра на единицу больше предыдущей. Запрещено цифры обозначать с помощью других цифр. Количество цифр называется основанием позиционной системы счисления.
Например, рассмотрим представление чисел в 16-ричной системе счисления. В качестве основания будет выступать число 16. Кроме этого, надо определить знаки, которые мы будем использовать в качестве цифр для записи чисел. Первые 10 цифр (от 0 до 9) мы можем позаимствовать из десятичной системы счисления. Остальные 6 цифр, соответствующих числовым значениям от 10 по 15, обозначим латинскими буквами A, B, C, D, E и F. Буква A будет обозначать цифру 10, буква B – цифру 11 и т.д.
Такое обозначение необходимо в связи с тем, что нельзя цифры обозначать с помощью знаков, обозначающих другие цифры.
Например, десятичному числу 168 будет соответствовать 16-ричное число A8. Действительно, 168 = 10·161 + 8·160. Поскольку 10 обозначается знаком A, то и получаем
Обратное преобразование из 16-ричного представления числа в десятичное также не представляет трудностей. Например, 16-чному числу 12316
будет соответствовать десятичное число 29110, поскольку в десятичной системе
В десятичной системе счисления 10 цифр от 0 до 9 (основание равно 10). Если в качестве основания задать другое число, то получим другую систему счисления. Любое количество можно представить в виде числа в различных системах счисления, и эти представления будут строго соответствовать друг другу.
Например, в 8-ричной системе счисления
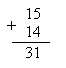 .
.Действительно, сложение 5 + 4 даст нам 10-чное 9, то есть 8-ричное 11. Следовательно, в последней позиции получаем 1 и запоминаем 1, которое складывается с 1 и 1, то есть в соседней левой позиции получаем 3. Если перевести 8-ричные 15 и 14 в привычную нам 10-чную форму (13 и 12), проделать сложение и результат (25) опять перевести в 8-ричное представление, то можно убедиться, что результат верен.
Арифметические действия в любой системе счисления выполняются аналогично тому, как это делается в 10-чной системе. Следует лишь учитывать величину основания.
Например, 10-чное 5 будет представлено двоичным числом 101. Действительно,
Максимальное двоичное число, состоящее из 4 битов, – это 1111. Следовательно,
Как мы уже говорили, наименьшей единицей измерения информации является бит, который представляет значения 0 или 1, поэтому в компьютере все данные представляются в двоичной системе счисления. Заметим, что четырьмя битами можно представить 16 десятичных чисел от 0 до 15.
Например, изменить информацию в памяти ЭВМ без использования той программы, с помощью которой эта информация была записана.
Обычно программы при взаимодействии с человеком преобразовывают данные из двоичного представления в привычную 10-чную или символьную форму. Однако нередко в процессе работы с ЭВМ требуется прочитать или записать информацию в компьютерном представлении. Делать это в двоичной форме, конечно же, утомительно и неудобно. Требуется какая-то более краткая запись, которая была бы более или менее удобна как компьютеру, так и человеку. В качестве такой краткой записи при просмотре или записи двоичных данных используется 16-ричная система счисления.
16-ричная система счисления – это разумный компромисс между тем, что удобно машине, и тем, что удобно человеку. Программы, обеспечивающие “непосредственную“ работу человека с памятью, при взаимодействии с человеком автоматически преобразовывают двоичное представление данных в 16-ричное (для человека) и обратно (для компьютера).
Четырьмя битами можно представить 16 чисел (от 0 до 15). Поэтому 16-ричное представление удобно, поскольку любое данное, записанное в одном байте, представляется всего двумя 16-ричными цифрами, первая из которых соответствует первой четверке битов, а вторая цифра – второй четверке битов. В этом и состоит причина использования 16-ричной системы.