Пусть на плоскости имеются фигуры G и g, причем ![]() (рис. 1).
(рис. 1).
.jpg)
Рис. 1. Фигуры G и g
На фигуру G наугад бросается точка. Это означает выполнение следующих предположений:
1) брошенная точка может оказаться в любой точке фигуры;
2) вероятность попадания точки на фигуру g пропорциональна площади этой фигуры и не зависит от ее расположения относительно фигуры G.
Определение 3. (Геометрическое определение) Вероятность попадания наудачу точки на фигуру g (событие A) равна отношению площадей фигур g и G, т.е.
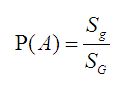 .
.
Замечание 4. В случае, когда g и G – отрезки прямой, вероятность события A равна отношению длин этих отрезков. Если g и G – тела в трехмерном пространстве, то вероятность события A находят как отношение объемов этих тел. Поэтому в общем случае
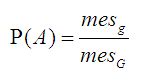 ,
,
где mes – метрика рассматриваемого пространства.
Замечание 5. Геометрическое определение вероятности применяется к испытаниям с бесконечным числом исходов.
Пример 2. (Задача о встрече) Два лица договорились встретиться в определенном месте между 12 и 13 ч., причем каждый пришедший на встречу ждет другого в течение 20 мин., но не дольше, чем до 13.00, после чего уходит. Найти вероятность встречи этих лиц, если каждый из них приходит в случайный момент времени, не согласованный с моментом прихода другого.
Решение. Пусть событие A – встреча состоялась. Используя определение 3, получим
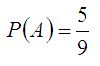 .
.
Решение. Пусть событие A – встреча состоялась. Обозначим через x – время прихода первого лица на встречу, y - время прихода второго лица. Тогда множество всех возможных исходов опыта – множество всех пар (x, y), где
![]() .
.
А множество благоприятствующих исходов определяется неравенством
![]() (мин).
(мин).
Оба этих множества бесконечны, поэтому классическое определение для вычисления вероятности применить нельзя. Воспользуемся геометрическим определением. На рис. 2 изображены множества всех возможных исходов (квадрат OKMT) и благоприятствующих исходов (шестиугольник OSLMNR).
Используя определение 3, получим
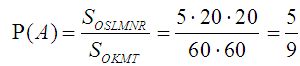 .
.
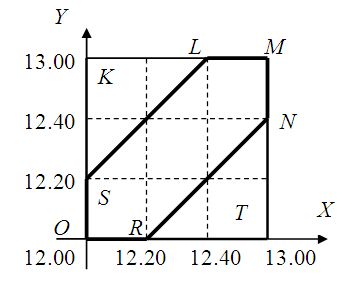
Рис. 2. Задача о встрече. Множества всех исходов
и благоприятствующих исходов