Обыкновенные дифференциальные уравнения возникают во многих задачах естественных наук. Чаще всего встречается задача Коши: отыскать некоторую функцию y(x), удовлетворяющую дифференциальному уравнению

и некоторым начальным условиям: y(x₀) = y₀,y⁽¹⁾(x ₀) = y₀⁽¹⁾y⁽ⁿ⁻¹⁾(x ₀) = y₀⁽ⁿ⁻¹⁾. Например, в общей физике наибольший интерес представляют дифференциальные уравнения второго порядка. Схема решения задачи Коши в MATLAB следующая:

1. Приведение уравнения n-го порядка к n уравнениям первого порядка. Это необходимо для задания вектора правых частей дифференциального уравнения. Размерность вектора равна порядку старшей производной;
2. Написание функции, задающей вектор правых частей системы дифференциальных уравнений первого порядка. Следует обратить внимание, что простое использование вектора вызовет ошибку во всех решателях;
3. Вызов решателя с нужными аргументами – вектором начальных условий и функцией правых частей системы уравнений.

Дальнейшая работа с полученными данными возможна обычными средствами MATLAB. Краткий синтаксис вызова решателя следующий: [x,y]=ode(function,x0,y0). Слева от знака равенства указаны выходные данные функции, которые будут вычислены обращением к решателю ode, y0 – вектор начальных условий, x0 – вектор значений независимой переменной. Расширенный синтаксис вызова решателей позволяет установить дополнительные опции, например абсолютную (по умолчанию 10⁻⁶) и относительную (по умолчанию 10⁻³)погрешности, шаг интегрирования и др. Удобный способ задания всех таких опций предоставляет структура odeset. Вызов odeset без аргументов приведет к выводу всех полей этой структуры и их значений по умолчанию. Предварительное определение такой структуры командой вида opt=odeset(’name’,value) позволяет в дальнейшем при вызове решателя в качестве одного из аргументов указать opt.

Рассмотрим в качестве примера решение уравнения движения для тела, брошенного под углом к горизонту с некоторой скоростью. Если пренебрегать сопротивлением воздуха, то решение этой задачи прекрасно знает любой школьник – траекторией движения тела будет парабола. Для решения нам потребуется два дифференциальных уравнения второго порядка – по одному для каждой координаты:

В качестве начальных значений выберем начальные координаты? равными нулю, а первые производные этих координат – равными 10. Для формирования вектора правых частей дифференциального уравнения нам потребуется определить две новых функции (в обычном понимании) – по порядку уравнения. Введем обозначения: y₁ = y и y₂ = y₁^′. В новых функциях вторая производная от координаты будет представлена как первая производная от вспомогательной функции y1 и уравнение второго порядка для координаты y будет сведено к системе двух уравнений первого порядка:

По своему физическому смыслу y₂ – это скорость тела вдоль вертикальной оси. Вектор начальных условий для системы дифференциальных уравнений тогда будет иметь вид y0=[0;10]. Для корректного решения вектор должен быть столбцом, поэтому элементы вектора отделены не пробелом, а точкой с запятой. Первое значение – начальная координата, второе – начальная (вертикальная) скорость. Функцию первый аргумент решателя сформируем с помощью оператора @ – yt=@(t,y)[y(2);-10]. В круглых скобках указаны выходные параметры функции, а вектор-столбец есть вектор коэффициентов правых частей системы дифференциальных уравнений. В качестве решателя используем ode45, реализующий метод Рунге-Кутты 4 порядка – [to,yo]=ode45(yt,ts,y0). Выходными значениями [to,yo] являются вектор значений времени to и массив, содержащий координаты и скорости вдоль вертикали. Аналогичным образом преобразуется уравнение для горизонтальной координаты. Поскольку выходные массивы xo и yo содержат два вектор-столбца, то из них предварительно выделены столбцы, соответствующие координатам. В конце построен график зависимости одной координаты от другой – траектория тела.

 

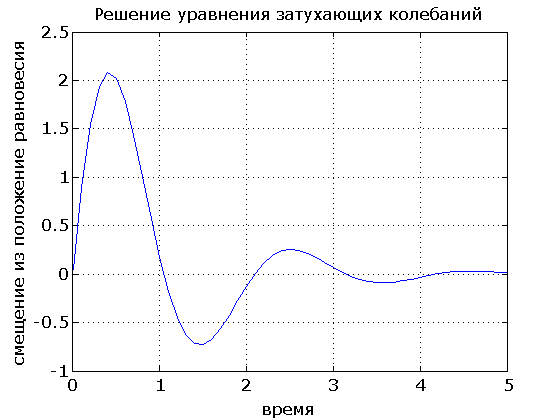
В качестве дополнительного примера можно рассмотреть решение уравнения затухающих колебаний: y^′′ + 2βy^′ + ω²y = 0 (пусть 2β = 5, а ω² = 10). Снова определяя вспомогательные функции в виде y₁ = y и y₂ = y₁^′, получим вектор для правых частей двух дифференциальных уравнений в виде [y(2);-2*y(2)-10*y(1)]. Пример 41 строит зависимость координаты затухающих колебаний от времени.

В MATLAB присутствует несколько решателей (solver) обыкновенных дифференциальных уравнений. Формат вызова практически всех решателей одинаков, аргументы также имеют одинаковый смысл. Для начала численных экспериментов с дифференциальными уравнениями рекомендуют использовать решатель ode45 и, только если этой функцией построить решение не удается, следует выбрать более подходящий для задачи решатель. Также если ode45 обеспечивает слишком высокую точность, а скорость работы, наоборот, низкую, то есть смысл выбрать другой решатель – ode23. Выбор решателя, обеспечивающего приемлемую точность за приемлемое время вычислений, определяется характером поведения искомой функции на интервале интегрирования. Ни один из решателей не является встроенной функцией, и это значит, что можно посмотреть и использовать его код для модификации стандартных решателей под конкретные задачи.