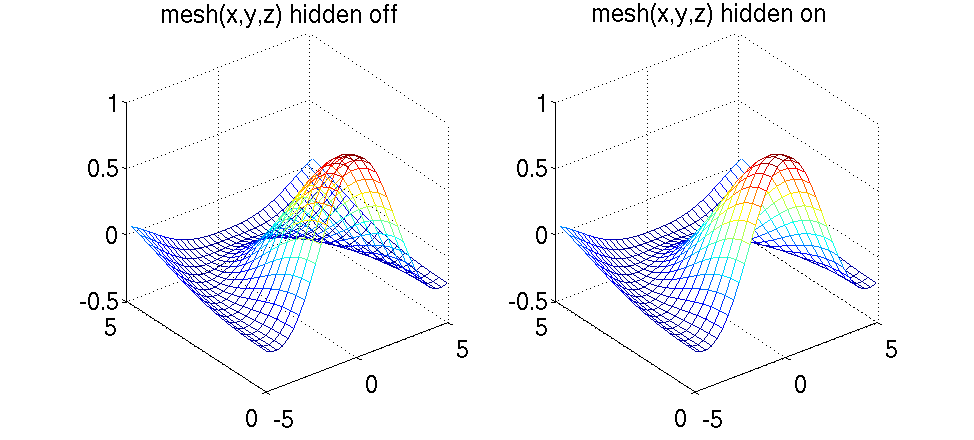
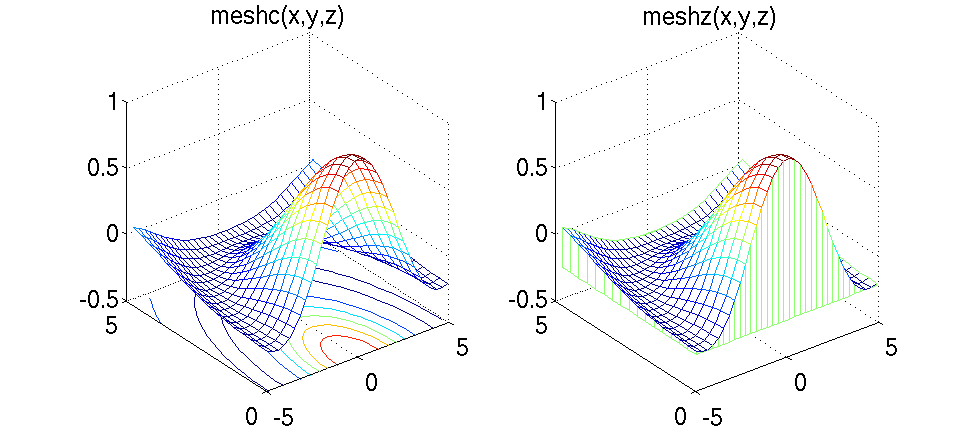
Для построения графика функции от двух аргументов нужно заранее подготовить матрицы значений двух аргументов для прямоугольной области плоскости XY , в которой в дальнейшем и будет строиться график. Чаще всего для создания таких матриц используют специальную функцию MATLAB meshgrid. Синтаксис её вызова следующий: в качестве входных параметров должно быть указано два массива, в качестве аргументов допускается указывать один, и тогда область будет не прямоугольной, а квадратной с одинаковым шагом изменения по каждой оси. Для непосредственного построения графика функции двух аргументов пользуются чаще всего двумя командами – surf и mesh. Обе строят поверхности в пространстве, причём surf строит именно поверхность, а mesh – только каркасные линии. У каждой из mesh и surf есть еще по два варианта вызова с постфиксом -z и -с. Meshc строит, кроме каркаса, линии равного значения функции на координатной плоскости XY , meshz добавляет эффект "водопада закрашивая место между поверхностью и координатной плоскостью XY . У функции mesh есть опция hidden off/on, вариант hidden off делает поверхность прозрачной. У функции surf есть опция shading flat, позволяющая сделать линии каркаса невидимыми, и shading interp, производящая дополнительно сглаживание поверхности.
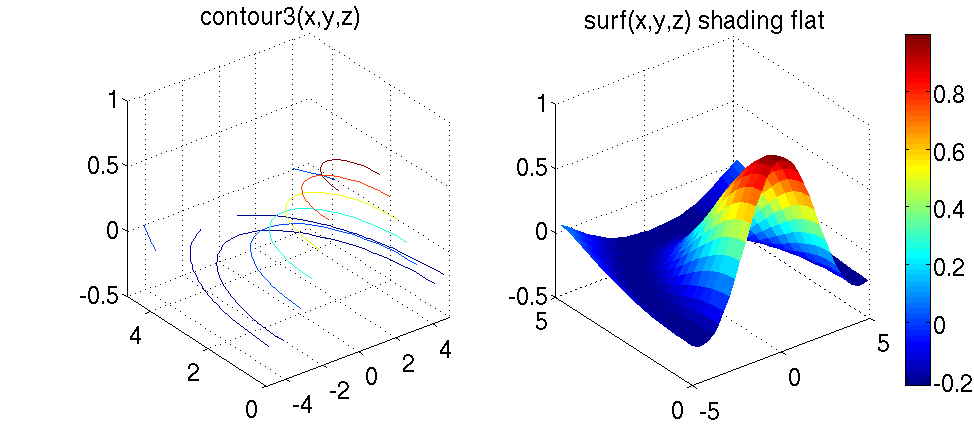
Для трехмерных функций, заданных параметрически, существует специальная команда построения графиков – plot3. Синтаксис её вызова ничем не отличается от всех остальных подобных, но существуют специальные опции, связанные со свойствами линии, – толщина, тип, цвет и прочее. Еще одна специальная функция для отрисовки графиков в пространстве призвана строить пространственные линии уровня – contour3. Для всех функций можно указать дополнительно параметр colorbar, который приведёт к добавлению в графическое окно вертикальной линии с градиентной окраской и нанесенными рядом с ней значениями функции. Палитру, которая будет использоваться для градиентной заливки шкалы, можно изменять командой colormap. Пример 23 демонстрирует включение дополнительных опций для построения и оформления графиков. Как видно из текста, в качестве таких опций можно задать множество параметров оформления. Удобнее всего для этих целей использовать функцию set, устанавливающую разные параметры.
Пример 23. График двумерной функции
 с разными опциями. Сценарий специально разбит на ячейки.
с разными опциями. Сценарий специально разбит на ячейки.2 r=sqrt(x.^2+y.^2);
3 z=sin(r)./r;
4 %%
5 subplot(1,2,1);mesh(x,y,z);title(’mesh(x,y,z)␣hidden␣off’);
6 set(gca,’FontSize’,18);hidden off;
7 subplot(1,2,2);mesh(x,y,z);title(’mesh(x,y,z)␣hidden␣on’);
8 set(gca,’FontSize’,18);hidden on
9
10 %%
11 subplot(1,2,1);meshc(x,y,z);title(’meshc(x,y,z)␣’);
12 set(gca,’FontSize’,18);
13 subplot(1,2,2);meshz(x,y,z);title(’meshz(x,y,z)’);
14 set(gca,’FontSize’,18);
15
16 %%
17 subplot(1,2,1);surf(x,y,z);title(’surf(x,y,z)’);
18 set(gca,’FontSize’,18);
19 subplot(1,2,2);surf(x,y,z); title(’surf(x,y,z)␣shading␣interp’);
20 set(gca,’FontSize’,18);shading interp
21
22 %%
23 subplot(1,2,1);surf(x,y,z);title(’surf(x,y,z)’);
24 set(gca,’FontSize’,18);
25 subplot(1,2,2);surf(x,y,z); title(’surf(x,y,z)␣shading␣flat’);
26 set(gca,’FontSize’,18);shading flat
27
28 %%
29 subplot(1,2,1);contour3(x,y,z);title(’contour3(x,y,z)’);
30 set(gca,’FontSize’,18);
31 subplot(1,2,2);surf(x,y,z); title(’surf(x,y,z)␣shading␣flat’);
32 set(gca,’FontSize’,18); shading flat; colorbar