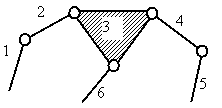
Определение степени подвижности механизма
Числом ведущих звеньев определяется степень подвижности механизма, или число его степеней свободы относительно стойки.
Итак, известно, что в кинематической цепи (КЦ) могут быть КП 1…5 классов: Р1, Р2, Р3, Р4, Р5. Число степеней свободы отдельного звена, не связанного с другими, равно 6. Если число звеньев КЦ k, тогда число степеней свободы 6k. Отсюда надо отнять число степеней свободы, которые отнимаются вхождением звеньев в КП, таким образом, число степеней свободы Н, которыми обладает КЦ:
H=6k–5P5–4P4–3P3–2P2–P1. (1.1)
Обычно рассматривается число степеней свободы механизма относительно неподвижного звена (стойки):
W=H–6=6(k–1)–5P5–4P4–3P3–2P2–P1.
Пусть k–1=n – число подвижных звеньев КЦ, тогда
W=6n–5P5–4P4–3P3–2P2–P1. (1.2)
Эта формула носит название Сомова–Малышева (Сомов П.И., 1887, Малышев А.П., 1923), формула подвижности или структурная формула кинематической цепи общего вида.
Данная формула применима в том случае, если на движение звеньев, входящих в состав механизма, не наложено каких-либо общих дополнительных условий.
В частном случае плоского механизма (когда все звенья движутся параллельно одной общей плоскости) на движение в целом наложено три общих ограничения, структурная формула принимает вид (формула Чебышева):
Для твердого тела, свободно движущегося в пространстве, число степеней свободы равно шести: три поступательных вдоль осей х, у, z и три вращательных вокруг этих осей. Для звеньев, входящих в кинематическую пару, число степеней свободы всегда меньше шести, так как условия соприкосновения (связей) уменьшают число возможных перемещений одного звена относительно другого: одно звено не может внедряться в другое и не может от него удаляться.
Число степеней свободы равно числу обобщенных координат системы, если все связи в системе геометрические и, следовательно, налагают ограничения только на положения звеньев. Число обобщенных координат такое, чтобы однозначно определить положение всех элементов (звеньев) системы.
Число степеней свободы пространственного механизма определяют с помощью формулы (Сомова–Малышева)
W=6n–5P5–4P4–3P3–2P2–P1,
где n – число подвижных звеньев; Р1…Р5 – число кинематических пар соответствующего класса.Номер семейства равен числу общих условий связи, которые наложены на все звенья механизма.
Связи (условия связи) – ограничения условия, которые не позволяют точкам материальной системы занимать произвольные положения в пространстве и иметь произвольные скорости.
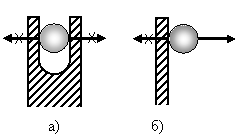
Различают связи удерживающие, которые характеризуются ограничениями, как для возможного сближения точек (тел), так и возможного их относительного удаления (сх. а), и неудерживающие, которые характеризуются односторонними ограничениями (например, только для относительного сближения – сх. б). Удерживающие связи характеризуются также ограничениями скорости как по верхнему, так и по нижнему пределу, а неудерживающие связи – односторонними ограничениями, т.е. только по одному из пределов.
Связи могут быть также стационарными (склерономными), не зависимыми от времени, и нестационарными (реономными), зависимыми от времени.
Связи, накладывающие ограничения только на перемещения, называют геометрическими (голономными), а связи, накладывающие ограничения на перемещения и скорости, называют кинематическими.
Если ограничения кинематических связей нельзя привести к ограничениям только на перемещения, то такие связи называют неголономными (неинтегрируемыми).
Цепь кинематическая – связанная система звеньев механизма, образующих между собой кинематические пары.