Этот метод позволяет определить величину уравновешивающей силы без определения реакций в кинематических парах, т. е. без выполнения силового расчета групп Ассура.

Рычаг Жуковского представляет повернутый на 90º план скоростей, принимаемый как твердое тело, с неподвижной точкой в полюсе, к концам векторов одноименных точек которого приложены внешние силы, в том числе уравновешивающая сила. Из условия равновесия этого рычага и определяется величина уравновешивающей силы.

На рис. 3.11 показан повернутый на 90º план скоростей с приложенными к концам соответствующих векторов внешними силами.

Момент сопротивления M₅, а также моменты сил инерции M_i5 и M_i2 звеньев 5 и 2 на рычаге Жуковского заменены парами сил , приложенными в точках K и E, перпендикулярными звену 5, и силами приложенными в точках В и D перпендикулярно звену 2 (рис. 3.11,б, в). Значения этих сил определятся из выражений:

(3.19)

(3.20)

(3.21)

Принимая повернутый на 90º план скоростей как твердое тело (рычаг), напишем уравнение равновесия

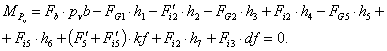(3.22)

Рис. 3.11. Рычаг Жуковского

Из этого уравнения и определится уравновешивающая сила F_b. (Заметим, что в этом уравнении «плечи» сил P_vb, kf, df, h₁, h₂, … могут определяться непосредственно по чертежу.)

Расхождения в значениях величины уравновешивающей силы, полученных из плана сил и рычага Жуковского, определяемые по формуле

, (3.23)

обычно не превышают 5…7 %.

Результаты определения реакций в кинематических парах и уравновешивающей силы удобно свести в таблицу.