Структурная классификация плоских шарнирных механизмов была разработана русским ученым профессором Л.В. Ассуром (1914 г.), а затем развита И.И. Артоболевским (PowerPoint – Р1).
Согласно классификации Л.В. Ассура каждый плоский механизм состоит из начальных механизмов и присоединенных к ним структурных групп (групп Ассура) с нулевой степенью подвижности.
Начальными механизмами могут быть:
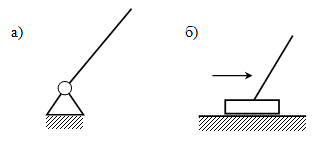
а) начальный вращательный механизм (рис. 1.14, а):
n=1, Р5=1 (В12), Р4=0, W=1;
б) начальный поступательный механизм (рис. 1.14, б):
n=1, Р5=1 (П12), Р4=0, W=1.
 |
|
Рис. 1.14. Начальные механизмы |
Начальные механизмы относятся к механизмам 1-го класса.
Основной принцип образования механизмов заключается в последовательном наслоении кинематических цепей, обладающих определенными структурными свойствами.
Группой Ассура называется кинематическая цепь с нулевой степенью свободы относительно тех звеньев, с которыми входят в кинематические пары свободные элементы ее звеньев, и не распадающаяся на более простые цепи, обладающие также нулевой степенью свободы.
Равноправно и следующее определение: группой Ассура называют элементарную кинематическую цепь, которая в случае ее присоединения элементами внешних пар к стойке получает нулевую степень подвижности:
W=3n–2P5–P4=0.
Рассмотрим, при каком соотношении между числом подвижных звеньев n и кинематическими парами Р5 и Р4 могут существовать группы Ассура:
а) для групп Ассура только с кинематическими парами 5-го класса степень подвижности определяется:
W=2n–2P5, следовательно, n= `(2)/(3)`P5
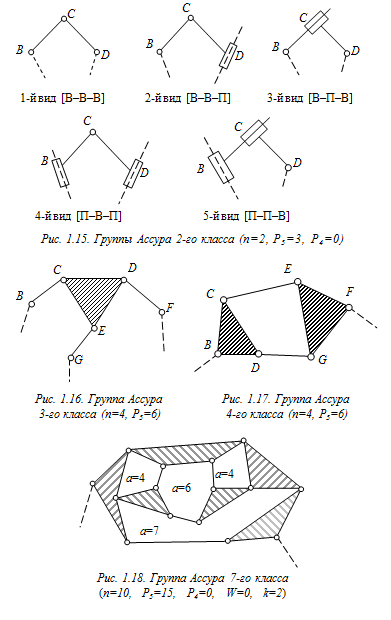
Возможные сочетания чисел звеньев и кинематических пар (рис. 1.15‑1.18):
| n | 2 | 4 | 6 | 8 | … |
| Р5 | 3 | 6 | 9 | 12 | … |
б) для групп Ассура с КП 5-го и 4-го классов:
W=3n–2P5–P4.
| n | P5 | P4 |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| … | … | … |
Назовем звено и стойку, образующие кинематическую пару 5-го класса, механизмом 1-го класса.
 |