Разделим процесс дискретизации на две части:

разбиение объекта на элементы;
нумерация элементов и узлов.

Дискретизация одномерного объекта сводится к делению отрезка на более короткие участки, при этом варьировать можно только количество этих участков и их размеры. Отметим, что иногда, в соответствии с природой протекающего процесса, эффективным оказывается деление на участки разной длины.

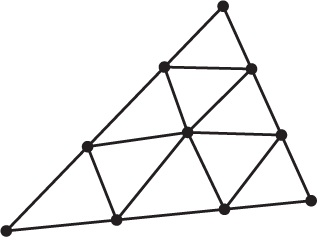
Нетривиальной задача становится уже в двухмерном случае. Рассмотрим разбиение двухмерной области на линейные треугольные элементы. Треугольник – это простейший элемент из двухмерных элементов в смысле аналитической формулировки, следовательно, при моделировании области треугольниками можно использовать наибольшее число элементов. Любые другие элементы можно представить в виде комбинации треугольников, поэтому деление области на треугольники – как правило, наилучший способ разбиения. В большинстве случаев при разбиении производится деление на четырехугольные и треугольные подобласти, или зоны, которые затем подразделяются на треугольники. Стандартная процедура разбиения заключается в следующем: необходимо выбрать определенное число узлов вдоль каждой стороны и соединить соответствующие узлы прямыми линиями, а точки пересечения этих линий считать узлами. Например, треугольная зона, разбитая на девять элементов после размещения четырех узлов на каждой стороне, показана на рис. 6а. Узлы на сторонах зоны можно располагать на разных расстояниях, что позволяет варьировать размеры элементов. В случае криволинейной подобласти, границы ее элементов заменяются на прямые отрезки (рис. 6б).


а	б

Рис. 6. Простейшие варианты разбиения на конечные элементы. Отметим, что на рисунке б штриховой линией представлена исходная форма, а сплошными линиями изображены элементы

Число треугольных элементов в результате разбиения равно (n − 1)², где n – количество узлов на стороне треугольной подобласти.

Отметим, что случай разбиения на четырехугольные элементы можно простым образом свести к разбиению на треугольники. Для этого достаточно провести короткую диагональ в каждом внутреннем четырехугольнике. Разбиение с использованием короткой диагонали предпочтительно, потому что элементы, близкие по форме к равностороннему треугольнику, приводят к более точным результатам, чем длинные узкие треугольники. Четырехугольные зоны обычно разбивают на элементы соединением узлов на противоположных сторонах. Число узлов на смежных сторонах четырехугольника может быть различным. Если сеть разбиения измельчается или укрупняется, то на противоположных сторонах может быть разное число узлов, иначе число узлов должно быть одинаковым. Расстояние между граничными узлами можно варьировать, чтобы получать элементы различных размеров. В четырехугольнике будет 2(n− 1)(m− 1) элементов, если на его смежных сторонах фиксировано n и m узлов.

Равномерное разбиение, когда все элементы имеют одинаковую форму и размеры, обычно не проводится, потому что существуют концентрация напряжений, температурные градиенты и т.д. В этом случае возможность варьировать размеры элемента в методе конечных элементов позволяет наиболее простым способом, применяя четырехугольные подобласти с неравным числом узлов на противоположных сторонах, проводить процедуру дискретизации неравномерно. Например, расположив два узла на одной стороне против трех узлов на противоположной стороне. Проиллюстрируем применение изложенных идей дискретизации с помощью разбиения модели прямоугольной и круглой областей в COMSOL multiphysics (рис. 7).


а	б

Рис. 7. Пример разбиения, причем способ разбиения повторяет геометрию фигуры

Для сохранения непрерывности рассматриваемых величин вдоль общей границы элементов необходимо, чтобы треугольная и четырехугольная подобласти имели общую границу, число узлов на этой границе для обеих подобластей должно быть одинаковым, а относительное положение узлов должно совпадать. Расстояния между узлами вдоль границ четырехугольной зоны изменяются так, чтобы элементы вблизи криволинейной части границы были малыми (рис. 8).


а	б

Рис. 8: а – разбиение некоторой области с учетом ее нетривиальной геометрии, т.е. плотность конечных элементов в особых областях выше, чем в других; б – искусственным образом добавлена особенность в виде окружности (такая особенность может быть связана с физикой явления)

Во многих задачах необходимо отметить подобласти (узлы, направления, траектории и т.д.), которые обладают определенными преимуществами над другими. Границы между подобластями должны проходить там, где изменяются геометрия, приложенная нагрузка или свойства материала. Как правило, в этих подобластях разбиение необходимо сильно измельчить. Например, на рис. 8б показано разбиение области (рис. 8а) с учетом некоторой особенности заданной на окружности. В качестве такой особенности может выступать сильный градиент искомой двухмерной функции вблизи окружности. Подобное разбиение позволяет с достаточной эффективностью и минимумом затрат расчетной мощности значительно увеличить точность расчетов.

Многие физические задачи не имеют четко установленных границ области анализа. Моделирование тел, бесконечно протяженных в одном или нескольких направлениях, представляет собой определенную задачу о граничных условиях.

Вторая часть процесса дискретизации (нумерация узлов) влияет на эффективность вычислений. Использование метода конечных элементов приводит к задаче решения системы большого числа линейных алгебраических уравнений. В большинстве случаев матрица коэффициентов системы имеет вид s- диагональной матрицы, т.е. все коэффициенты, не лежащие на этих диагоналях, равны нулю. Правильная вычислительная программа использует только ненулевые коэффициенты матрицы, поэтому наиболее эффективные способы решения таких систем универсализированы, и замечательным является то, что в настоящее время исследователям физических явлений не требуется писать сложные вычислительные системы, так как они реализованы в специализированных программных продуктах (в том числе в COMSOL).

Итак, при решении задач методом конечных элементов используются разнообразные элементы, и задача правильного разбиения области зависит от структуры моделируемой системы и процессов, протекающих в ней. Задание геометрии и правильное разбиение области являются одной из основных проблем при использовании специализированных программных продуктов по численному моделированию, а задача нумерации узлов реализована в этих программах.

Идеи, изложенные для двухмерной области в данном разделе, могут быть обобщены на случай трехмерного тела.