Рассмотрим несколько простейших задач, встречающихся в общем курсе физики. Важно отметить, что решение этих задач может быть получено без использования программных средств и метода конечных элементов. В сравнении результата, полученного на листке бумаги и вычисленного в комсол есть дополнительная методическая ценность. Подобные примеры дают достаточно много для освоения комсол – рассматривая простейшие задачи, проще научиться решать более серьезные.
Итак, первая задача из области электростатики. Пусть заданы два шара (из диэлектриков), в каждом из них заряд распределен равномерно по объему с некоторой плотностью ρ, но в одном шаре эта плотность положительная, а в другом отрицательная. Задача состоит в том, чтобы найти напряженность электрического поля в области пересечения этих шаров. Для простоты будем считать, что шары имеют одинаковый радиус. Элементарное решение этой задачи с использованием электростатической теоремы Гаусса приводит к тому, что в области пересечения электростатическое поле будет однородным. Попробуем этот же ответ получить в COMSOL Multiphysics.
Понятно, что решение данной задачи с привлечением уравнений в частных производных будет формулироваться как краевая задача для уравнения Пуассона. Запустим COMSOL Multiphysics и выберем трехмерную задачу. В Model Wizard используем уравнение Пуассона, а в качестве решателя следует указать – Stationary, поскольку решение от времени зависеть не будет. Построим геометрию в виде двух сфер с параметрами, которые выставлены по умолчанию, но для центра одной из этих сфер зададим значение, равное единице. Это обеспечит некоторую область перекрытия шаров. Геометрия задачи будет представлена тремя областями – в центре область пересечения шаров и две области по краям. В центральной части необходимо определить нулевую объемную плотность заряда. На крайних областях – равные по модулю отрицательную и положительную объемные плотности. В выбранной модели для этого нужно выбрать PDE в Model Builder и в General Form PDE в поле значения коэффицииента f указать ноль для центральной части, минус единицу для левой и единицу для правой области. Вместо единицы можно, конечно, выбрать другое значение.
Граничные условия для внешних границ следует указать соответствующими задаче Дирихле, а для внутренних – задаче Неймана. После этого нужно создать сетку. Поскольку задача вполне стандартная, то и выбор сетки не составляет труда. Далее, выбрав правой кнопкой мыши Study, в общем дереве модели запускаем решение задачи.
В результате внутри пункта Result будут созданы структуры, содержащие решение задачи. Нас, прежде всего, интересует соответствие численного решения тому представлению, которое складывается в результате решения на бумаге. Уравнение Пуассона сформулировано для потенциала электростатического поля. Как известно, напряженность электрического поля равна градиенту от потенциала, взятому с обратным знаком.
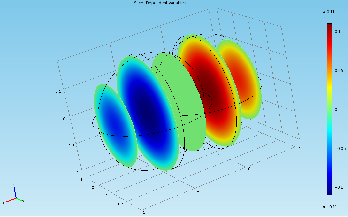
Посмотрим графическое представление решения для потенциала (рис. 83).
По умолчанию при решении данной задачи COMSOL Multiphysics создает два трехмерных графика. Первый – surface для дальнейшего анализа непригоден. Для анализа решения будем использовать второй созданный график – slice. Как видно из рис. 83, обычный вид этого графика не очень удобен.
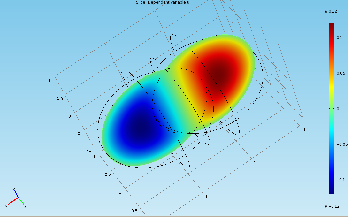
Выберем плоскость XZ для построения распределения потенциала в сечении области пересечения шаров и количество слоев установим равным единице (рис. 84).