Основная идея метода конечных элементов состоит в минимизация функционала вариационной задачи на множестве кусочно-непрерывных функций, каждая из которых определена на конечном числе подобластей. Кусочно-непрерывные функции определяются с помощью значений непрерывной величины в конечном числе точек рассматриваемой области.

В общем случае непрерывная величина заранее неизвестна, и нужно определить значения этой величины в некоторых внутренних точках области. Однако дискретную модель можно построить, если предположить, что числовые значения этой величины в каждой внутренней точке области известны. Для непрерывной величины поступают следующим образом:

В рассматриваемой области фиксируется конечное число точек. Эти точки называются узловыми точками, или узлами;
Значение непрерывной величины в каждой узловой точке считается переменной, которая должна быть определена;
Область определения непрерывной величины разбивается на конечное число подобластей, называемых элементами. Эти элементы имеют общие узловые точки и в совокупности аппроксимируют форму области;
Непрерывная величина аппроксимируется на каждом элементе полиномом, который определяется с помощью узловых значений этой величины. Для каждого элемента определяется свой полином, но полиномы подбираются таким образом, чтобы сохранялась непрерывность величины вдоль границ элемента.

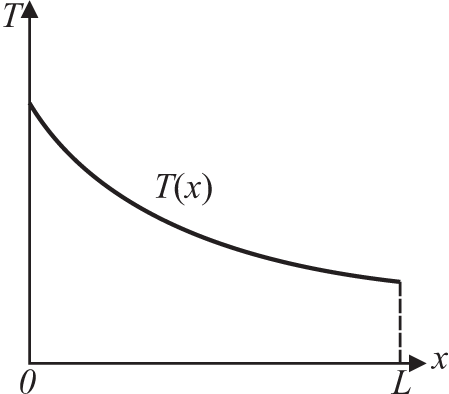
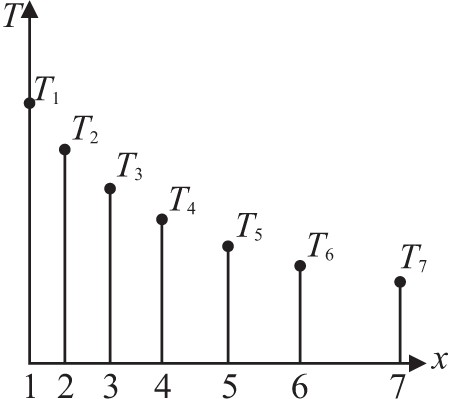
Рассмотрим стандартный пример распределения температуры T(x) в стержне длины L (рис. 1а). Зададим случайным образом семь точек на оси x, которым соответствуют некоторые известные значения T(x) (рис. 1б), и будем считать их узлами.


а	б

Рис. 1: а – распределение температуры в стержне, б – представление этого распределения в дискретном виде

Разбиение области на элементы можно провести несколькими способами: ограничить каждый элемент двумя соседними узловыми точками, образовав шесть элементов, разбить область на три элемента, каждый из которых содержит три узла, и т.д. Соответствующий элементу полином определяется по значениям T(x) в узловых точках элемента.

В случае разбиения области на шесть элементов, когда на каждый элемент приходится по два узла, функция элемента линейна по x, а аппроксимация T(x) состоит из шести кусочно-линейных функций, каждая из которых определена на отдельном элементе. В случае разбиения области на три элемента с тремя узловыми точками функции элемента можно представить в виде полинома второй степени, а аппроксимация T(x) будет состоять из совокупности двух кусочно-непрерывных квадратичных функций.

Для нахождения распределения температуры в остальных точках определяются множество узлов, а значения температуры в этих узлах являются переменными, так как они заранее неизвестны. Область разбивается на элементы, на каждом из которых определяется соответствующая функция элемента. Узловые значения T(x) необходимо отрегулировать таким образом, чтобы обеспечивалось наилучшее приближение к истинному распределению температуры. Это регулирование осуществляется путем минимизации некоторой величины (функционала), связанной с физической задачи (дифференциальным уравнением).

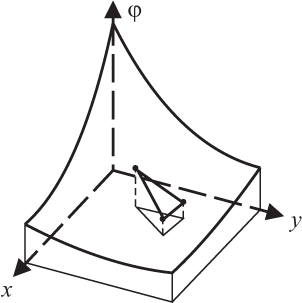
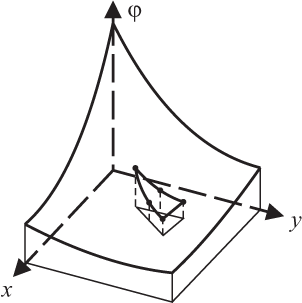
Процесс минимизации сводится к решению систем линейных алгебраических уравнений относительно узловых значений T(x). При построении дискретной модели непрерывной величины, определенной в многомерном случае (в системе COMSOL одно-, двух- и трехмерном), основная концепция метода конечных элементов используется аналогично, а в качестве элементов используются функции от нескольких переменных. Наиболее эффективный выбор элементов в двухмерном случае чаще всего осуществляется при использовании формы треугольника или четырехугольника. Функции элементов становятся плоскими поверхностями, если для данного элемента взято минимальное число узловых точек (рис. 2а), или криволинейными, если используемое число узлов больше минимального (рис. 2б). Отметим, что избыточное число узлов позволяет рассматривать элементы с криволинейными границами. Окончательной аппроксимацией двухмерной непрерывной величины будет служить совокупность кусочно-непрерывных поверхностей, каждая из которых определяется на отдельном элементе с помощью значений φ(x,y) в соответствующих узловых точках.


а	б

Рис. 2: а – треугольный элемент с тремя узлами, б – элемент с пятью узлами. Отметим, что элемент с пятью узлами с большей точностью повторяет геометрию поверхности, чем элемент с тремя узлами

Важной особенностью метода конечных элементов является возможность выделить из набора элементов такой, использование которого позволило бы определять функцию элемента независимо от его положения в общей связной модели и от других функций элементов. Задание функции элемента через произвольное множество узловых значений и координат позволяет использовать функции элемента для аппроксимации геометрии области.