После интенсивного ветрового перемешивания воды в водохранилище произошло ее замерзание. В 7 часов 1 декабря наблюдалось распределение температуры, показанное на рис.2 (кривая 1). Рассчитать, через сколько часов (суток) установится стационарный температурный режим, характеризующийся линейным распределением температуры (рис.2, кривая 2). Построить графики распределения температуры по глубине t = f (z) для отдельных моментов времени.

Исходные данные:

1)      глубина водохранилища h, ширина поперечного сечения В, расход воды Q;

2)       начальная температура воды t_н в момент замерзания τ₀;  

3)      теплоприток от грунта дна q_дн.

Пояснения к задаче

 В основе решения задачи лежит дифференциальное уравнение теплопроводности. Для решения этого уравнения целесообразно использовать метод конечных разностей. Расчетная формула этого метода (5.6) приведена в [1, с. 100], а также в пояснении к теме курсового проекта «Термический режим малопроточного водоема» [4, с.43].

 

  

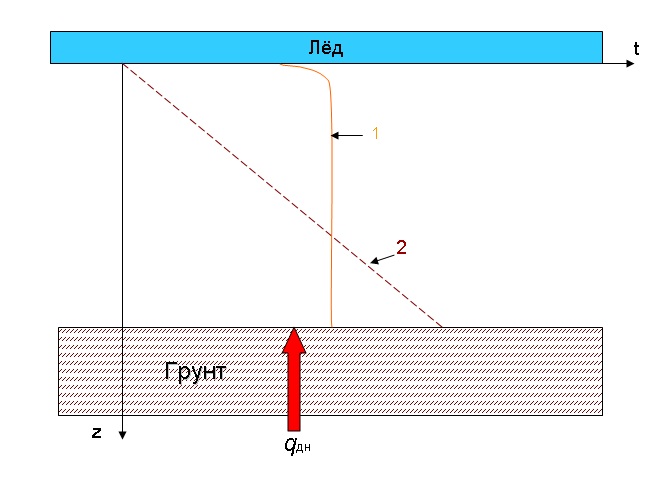
Рис. 2. Начальное - 1 и расчетное (стационарное) - 2 распределение температуры
по глубине водохранилища

 Порядок вычислений следующий. Прежде всего необходимо определить коэффициенты турбулентной теплопроводности λ_т и температуропроводности воды ɑ_т. Для расчета коэффициента λ_т воды при наличии ледяного покрова рекомендуется пользоваться формулой К. И. Россинского (2.24) [ 2 (Турбул. теплопроводность), с. 53]. При этом следует обратить внимание, что в пояснении к формуле допущена опечатка. Входящее в эту формулу значение удельного расхода воды, т. е. расхода, приходящегося на единицу ширины поперечного сечения водохранилища, необходимо подставлять в размерности м²/час, а не м²/с.

Коэффициент турбулентной температуропроводности рассчитывается по соотношению:                      

                                                                      ɑ_т  =  λ_т /( ρ_вс)                                                                             

 где с и ρ_в - соответственно удельная теплоемкость и плотность воды.

Далее необходимо установить, на каких глубинах и для каких моментов времени будет производиться расчет температуры воды. Применительно к данной задаче целесообразно задать следующие интервалы по глубине: Δz = 0,25 м для глубины 4 - 5 м и Δz = 0,5 м для глубины 6 - 10 м. Затем, используя условие Шмидта [1, с. 100]:

Δt/Δτ = ɑ_т Δ²t/ Δz²

вычисляем расчетные интервалы времени Δτ.

Для дальнейшего расчета необходимо на основе исходных данных записать начальные и граничные условия. На верхней границе, т. е. границе раздела вода - лед, температура воды постоянна в течение всего периода И равна 0 °С (граничное условие I рода).

На нижней границе (дне) задана плотность теплового потока от грунта к водной массе q_дн. Это так называемое граничное условие II рода. Используя закон теплопроводности,

q_дн = (Δt/Δz)|_z=h 

где Δt/Δz - градиент температуры воды в придонном слое (на глубине z=h), можно перейти к граничному условию I рода. Подставляя в условия Шмидта Δt = t|_z=h - t|_z=h-Δz получаем температуру воды на дне водоема:

t|_z=h= t|_z=h-Δz+ q_дн Δz/ λ_т

В этой формуле t|_z=h - температура воды на дне, т. е. при z=h, а t|_z=h-Δz - температура воды на глубине h-Δz, которая вычисляется
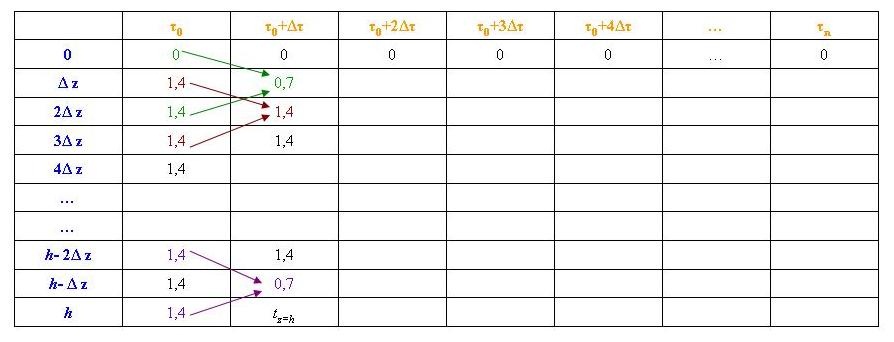
по расчетной формуле (5.6) [1] или [4, с.43]. Параллельно с расчетом температуры на нижней границе следует вести расчет температуры воды на заданных глубинах Δz, 2Δz и т. д. в определенные моменты времени τ₀ , τ₀+Δτ и т. д.,  где τ₀ - начальный момент времени, за который, согласно условию задачи, принимается 7 часов 1 декабря. Вычисления удобно производить в табличной форме (см. табл. 6). По результатам расчетов строятся графики распределения температуры по глубине t = f (z) для отдельных моментов времени. Для большей наглядности кривые t = f (z) следует построить в одних координатах с различными условными обозначениями (например, различными цветами).

Таблица 6

Расчет температуры методом конечных разностей