Водоем покрыт трехслойной снеголедяной толщей, состоящей из слоя свежевыпавшего снега, уплотненного снега и льда (рис. 1).  Допуская, что в первой декаде января наблюдается стационарный метеорологический режим, необходимо:

 1) вычислить плотность теплового потока q через снеголедяную толщу;

2) рассчитать значения температуры t₁,  t₂, t₃ на границах раздела слоев;

 3) построить график распределения температуры t = f (z);

4) подсчитать теплосодержание снеголедяной толщи площадью 1 м².

Исходные данные:

1) мощность слоя свежевыпавшего снега δ₁, мощность слоя уплотненного снега снега δ₂ = 0,05 м, толщина льда δ₃ = 0,20 м;

2) плотность соответствующих слоев снега: ρ_l и ρ₂ = 500 кг/м;

3) метеорологические данные: среднедекадные значения температуры воздуха θ₂ и скорости ветра U₂ на высоте 2 м в первой декаде января;

4) скорость течения воды в водохранилище подо льдом ν= 0,1 м/с.

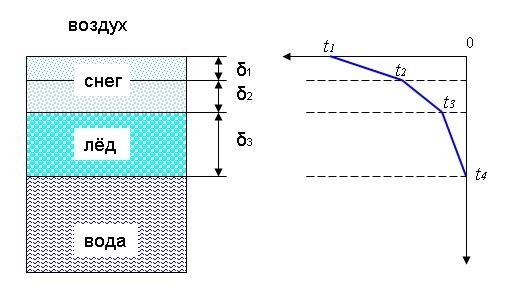
Рис. 1. Схема снеголедяной толщи и кривая зависимости t = f (z).

Пояснения к задаче

Для нахождения плотности теплового потока необходимо использовать формулу (3.42) [1, с. 69] или (2.24) [3 , с. 68]. Поскольку в задаче передача теплоты от воды к воздуху происходит не через один слой, а через трехслойную' толщу, в знаменатель указанной формулы следует вместо δ/λ - подставить величину Σ(δ_i/λ_i), где δ_i и λ_i - соответственно толщины и коэффициенты теплопроводности отдельных слоев, i - номер слоя. Формула (3.42) предназначена для расчета плотности теплового потока через стенку, материал которой не меняет свое агрегатное состояние. В нашей же задаче стенка состоит из льда - материала, меняющего свое агрегатное состояние, В связи с этим вся теплота, приходящая от воды ко льду, будет расходоваться на таяние его и за границу раздела (в толщу) не пройдет. Поэтому в  формуле (3.42) слагаемое 1/α₁ следует исключить.

Поскольку коэффициент теплопроводности снега зависит от его плотности, то значения λ₁ и λ₂ необходимо вычислить по формулам (2.58) и (2.59) [1; с. 45] или (1.35) и (1.36) [3; с. 46]. Значения коэффициента теплопроводности льда приведено в работах [1, с. 35] и [3, с.38]. Коэффициенты теплоотдачи от поверхности снега к воздуху рассчитываются по формуле (3.19) [1, с. 61] или [3; с.62] . Удельную теплоемкость снега и льда необходимо определить по формуле (2.42) [1, с. 35, 45] или (1.31) [3, с. 39], а плотность льда при п = 0 по формуле (2.36) [1, с. 33] или (1.27) [3, с. 37].

При расчете температур на границах раздела слоев следует иметь в виду, что при стационарном температурном режиме тепловые потоки через каждый из слоев равны между собой и равны вычисленному значению q, т.е. q₁ = q₂ = q₃ = q. Кроме того, необходимо учесть, что температура на границе раздела вода - лед равна  0 ^°С. Записывая плотность теплового потока через слой льда в соответствии с законом Фурье, можно рассчитать температуру t₃. Далее, рассматривая плотность теплового потока через слой уплотненного снега, рассчитывается температура t₂. Аналогичным образом находится температура на поверхности снега t₁ (см. [1, с. 83 - 84] или [3, с. 77-79]  ). По  результатам расчета температуры строится график её распределения по толщине снеголедяного покрова.