Проблема определения размеров и формы Земли  возникла в давние времена и остается актуальной в настоящее время. В каждую эпоху она решалась по-разному – средствами, специфическими для данного периода.

Уже в древние времена люди знали, что Земля круглая. Первым известным измерением формы Земли, при котором постулировалась ее шарообразность, было хорошо известное измерение Эратосфена(278 – 196 гг. до н.э.). Последующие уточнения этого представления о форме Земли были проведены после исследований Ньютона. На основе сформулированного им закона всемирного тяготения и учета действия центробежной силы он показал, что Земля должна иметь форму эллипсоида вращения.

При этом предполагалось, что Земля состоит из однородной идеальной жидкости. Ньютон определил также, каково будет сжатие полученного таким образом эллипсоида.

Дальнейшее развитие представлений о фигуре Земли произошло в 1873г. после публикаций работ немецкого геодезиста Е. Листинга. Он предложил рассматривать в качестве фигуры Земли уровенную поверхность, совпадающую на океанах с невозмущенной поверхностью воды, и продолженную под континенты по закону образования уровенных поверхностей, т.е. перпендикулярно к направлению полного вектора напряженности гравитационного поля. Эта поверхность была названа геоидом

 Задача определения фигуры Земли является одной из важнейших задач высшей и спутниковой геодезии. По современным взглядам под поверхностью Земли, понимают на суше физическую поверхность твердой оболочки Земли, а на морях и океанах - их невозмущенную поверхность. Вследствие чрезвычайной сложности физической поверхности Земли ее нельзя представить каким-либо математическим уравнением. Поэтому в высшей геодезии в качестве исходной координатной поверхности принимается более простые математические поверхности геоида и эллипсоида вращения. Поверхность геоида или основная уровенная поверхность - это уровенная поверхность, совпадающая с невозмущенной поверхностью мирового океана и мысленно продолженная под материками. Геоид не может быть определен геометрически. В геометрии нет такой поверхности и нет формул, ее выражающих. Эта поверхность связана только с Землей и обусловлена ее физическими свойствами, ее силовым полем. Она достаточно точно определяется на океанах, но не может быть определена точно на материках. Однако приближенно ее можно определить по гравитационному полю Земли.

Поверхность геоида имеет сложную, неправильную форму. Это связанно как с рельефом местности, так и с неравномерным распределением плотности  земных пород. Отступление геоида от эллипсоида колеблются от -107 до 85 м. Представление о геоиде дает рис.1, на котором изображены изолинии высот геоида относительно общеземного эллипсоида . 

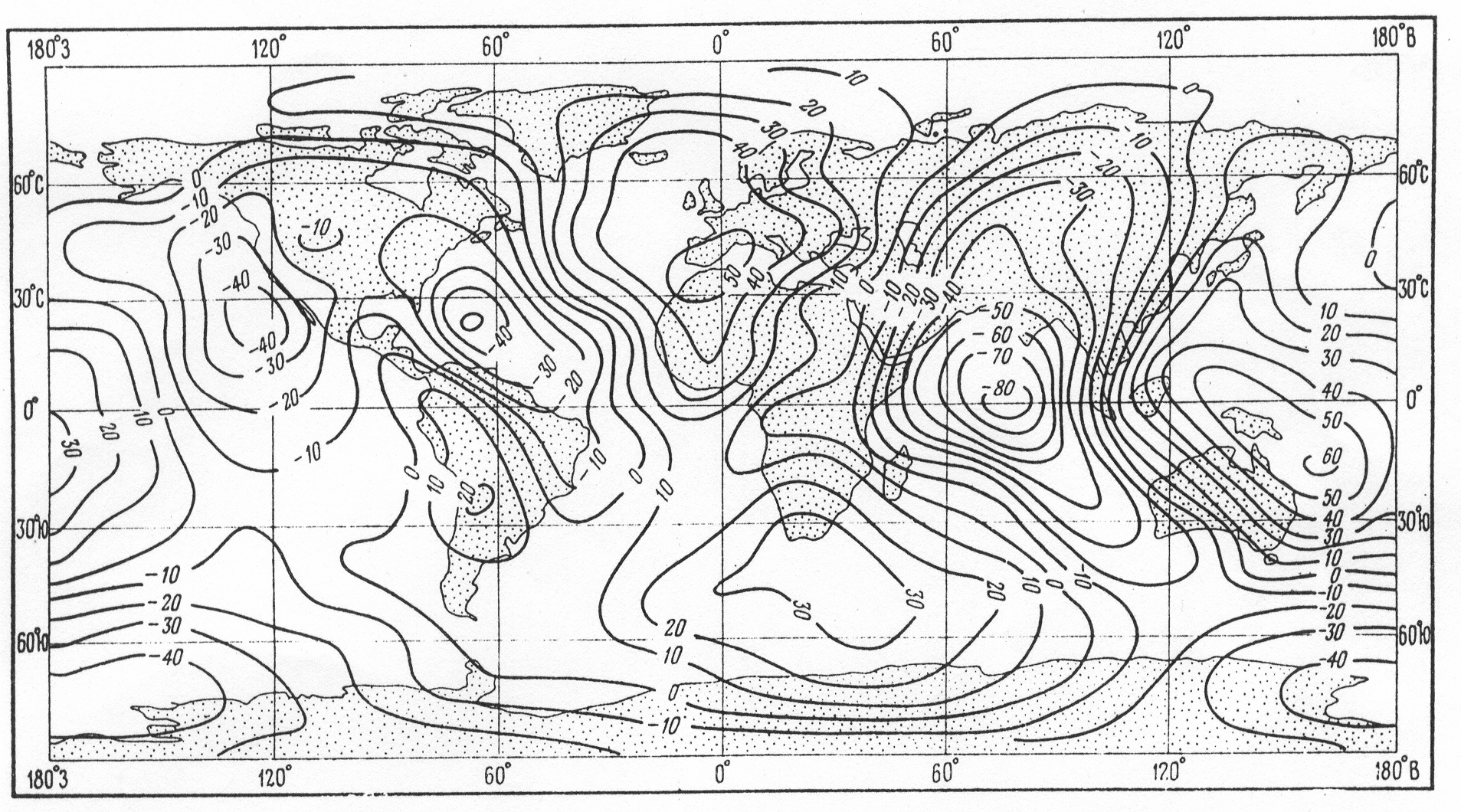
Рис 1. Карта геоида, приведенного к сжатию 1/298.25, построенная по результатам гравиметрических наблюдений на поверхности Земли и наблюдений за искусственными спутниками и при разложении потенциала по сферическим функциям до 14-го порядка включительно. Там, где наблюдения на поверхности Земли отсутствуют, использовались изостатические аномалии. Изолинии – высота в метрах над поверхностью сфероида. Превышения геоида соответствуют залеганию пород относительно высокой плотности, а понижения – породам пониженной плотности. Рисунок заимствован из книги Бота

В нахождении точек поверхности геоида и параметров эллипсоида наилучшим образом аппроксимирующий геоид заключается рассматриваемая нами задача.Считаем, что поверхность геоида представляет собой уровенную поверхность, заданную выражением  (см. |1,2 |)

            (1)

 Здесь  - экваториальный радиус Земли;   - геоцентрическая гравитационная постоянная (произведение гравитационной постоянной f и массы Земли М);   - сферические координаты точки на уровневой поверхности ( -геоцентрический радиус, то есть расстояние от центра масс Земли до искомой точки;  - геоцентрическая широта, т.е. дополнение до прямого угла образованного  и осью вращения Земли;  -геоцентрическая долгота, то есть угол между плоскостью меридиана, проходящего через , и плоскостью гринвичского меридиана);  и  - нормированные коэффициенты сферических гармоник;  - нормированные присоединенные функции Лежандра;   - угловая скорость вращения Земли.

При решении различных прикладных задач небесной механики, высшей и спутниковой геодезии, разложение по сферическим функциям в правой части выражения (1) всегда ограничиваются некоторой степенью N.

Параметры   определяются по спутниковым и гравиметрическим данным и нам известны. Также известны угловая скорость вращения Земли     и нормированные присоединенные функции Лежандра  , которые находятся по рекуррентным соотношениям.

Заданная таким образом приближенная аппроксимация выражения (1) будет описывать поверхность сглаженного геоида, который называется планетарным или глобальным геоидом. В нахождении точек поверхности такого геоида, его будем обозначать через G_N, и будет заключаться первая часть рассматриваемой задачи. Вторая часть задачи состоит в определении по известным точкам поверхности геоида параметров эллипсоида наилучшим образом аппроксимирующим геоид.