После нахождения множества точек глобального геоида можно определить параметры эллипсоида вращения, который наиболее лучшим образом вписывается в полученный нами геоид.

В этой задаче в качестве общеземного эллипсоида используется эллипсоид вращения. Каноническое уравнение этого эллипсоида вращения имеет вид

                                                                                                                      

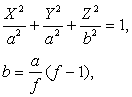
где X, Y, Z - координаты точек поверхности эллипсоида, a - большая полуось эллипсоида, b - малая полуось эллипсоида, f - знаменатель сжатия.

С помощью такой модели, зная параметры эллипсоида a и b, мы можем задать любую точку на поверхности эллипсоида через сферические координаты   и . Для этого воспользуемся соотношением перехода от сферических координат к прямоугольным координатам точки на поверхности эллипсоида

                                                                                                                 

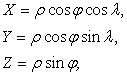
где  - расстояние от точки на поверхности эллипсоида до его центра.

Подставляя далее правые части соотношений в уравнение получаем искомое выражение для

                                                                                                    

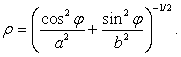
Теперь подробно рассмотрим метод нахождения полуосей эллипсоида. Суть метода заключается в том, чтобы найти такие значения a и b, для которых сумма квадратов всех отклонений точек геоида от точек эллипсоида была бы наименьшей.

Здесь возможны два варианта. Отклонения можно определить вдоль радиальных расстояний от центра геоида до точек его поверхности и по направлению высот точек геоида над поверхностью эллипсоида. Первый вариант является более простым. В данной работе рассматриваются оба способа. Алгоритм нахождения параметров эллипсоида сводится нами, в обоих способах, к решению задачи наименьших квадратов (НК) методом дифференциальных поправок.

1. Для первого способа описание алгоритма приведем в следующем виде. Для каждой точки геоида мы имеем из решения уравнения набор значений . Так же для каждой пары  и  можем определить расстояние  от точки на поверхности эллипсоида до его центра используя выражение () . Эти расстояния  рассматриваем, как функции от параметров a и b

                                                                                      

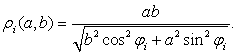
Далее находим значения параметров a и b как решение задачи наименьших квадратов (НК)

                                                                                               

Задача наименьших квадратов представляет собой задачу безусловной минимизации и может быть сведена к решению системы нелинейных уравнений

                                                                    

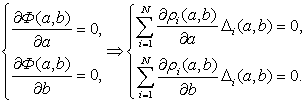
Здесь    - отклонения вдоль радиальных направлений -ых точек геоида от соответствующих точек эллипсоида. Система нелинейных уравнений может быть решена только численными итерационными методами. Для решения системы нами был использован метод дифференциальных поправок

                                                                                      

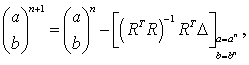
где

                                                            

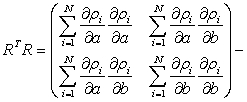
матрица нормальных уравнений,

   

                                                           

 

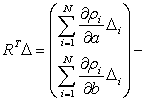
вектор свободных членов,  - номер итерации.

Решение задачи НК считается найденными, если выполняется следующее условие:

                                                                                                                          

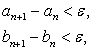
где -  заданная точность определения решения. При выполнении этого условия считаем, что решение задачи () суть  - приближение итерационного процесса (), то есть

                                                                  

Частные производные в методе дифференциальных поправок () определяются по следующим формулам

                                                                                          

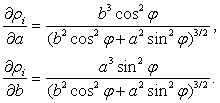
2. Аналогичным образом распишем задачу НК для второго способа определения параметров земного эллипсоида с использованием геодезических высот H. В этом способе вводятся геодезические координаты. В геодезической системе координат положение точки определяется геодезической высотой H над принятым земным эллипсоидом, геодезической широтой B и геодезической долготой  L. В нашем случае исходные точки задаются на поверхности геоида.

Связь прямоугольных и геодезических координат описывается выражениями

                                                                                                   

 

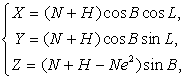
а также формулами обратного перехода

                                                               

 

 

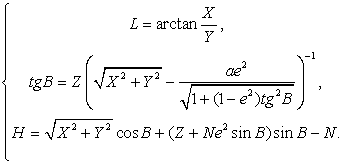
Здесь N –радиус кривизны первого вертикала, который вычисляется по формуле

                                                         

Задачу наилучшей аппроксимации поверхности геоида эллипсоидом будем рассматривать, в данном случае, как задачу НК вида

                                                                                                        

где  -высота   -ой точки геоида, .

Решение задачи осуществляем, как и ранее, методом дифференциальных поправок:

                                                                                      

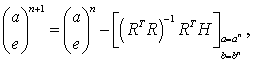
где

                                              

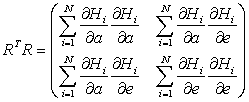
-матрица нормальных уравнений,

                                                       

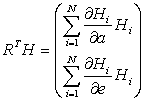
-вектор свободных членов;  

Здесь  - номер итерации; N- число точек на поверхности геоида.

Для численной реализации метода дифференциальных поправок найдем значения частных производных  и . Имеем

                                        

 

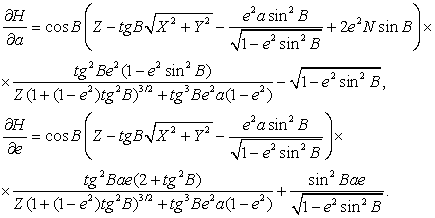
Частные производные в обоих способах можно также вычислить методом конечных разностей |5|. В этом  методе важно правильно выбрать шаг численного дифференцирования, что требует дополнительных вычислений и тем самым теряется его преимущество в простоте и универсальности по сравнению с аналитическим алгоритмом расчета частных производных. 

Следует также отметить, что рассматриваемые способы определения параметров аппроксимирующего эллипсоида с использованием радиальных расстояний и геодезических высот дают в пределах допустимой точности практически одинаковые решения  |2|. Одинаковы также свойства метода дифференциальных поправок в этих способах: скорость и область сходимости итерационных процессов. Представление о размерах и форме области сходимости дает рис.2. 

                               

                                  Область сходимости  

 

                                 

                                        

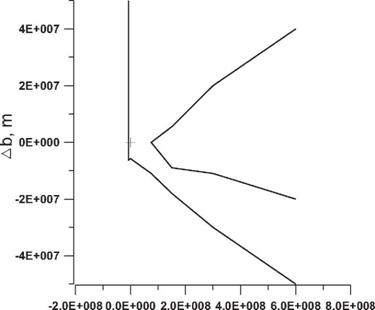
 Рис.2. Область сходимости итерационного метода дифференциальных поправок

 

Здесь  -отклонения начальных приближений  от НК-оценки .