Тема: Момент инерции тела человека относительно оси вращения в различных положениях.

Цель: Научиться определять момент инерции тела человека относительно оси вращения в различных положениях.

Задачи: Определить момент инерции тела человека относительно грифа перекладины в положениях:

1)   вис на перекладине.

2)   вис углом на перекладине.

Инструменты и оборудование: Тетрадь для лабораторных работ, карандаш, резинка, ручка или фломастер, линейка, микрокалькулятор.

Ход работы

Решение задачи 1

1. Нарисовать в декартовой системе координат кинематическую схему опорно-двигательного аппарата тела человека, в положении виса на перекладине (рис.1). Поместить центр масс кистей рук и гриф перекладины в начало системы координат. Ввести в схему, принятые в лабораторной работе 3, соответствующие обозначения для координат центра масс сегментов.

2. Уравнения для определения момента инерции системы тел имеют вид

 

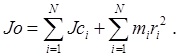                                                                                  (1)

 

Здесь J_O – момент инерции системы тел относительно оси вращения О; Jc_i – центральный момент инерции i-го тела; m_i - масса i-го тела; r_i – расстояние от центра масс i-го тела до оси вращения О; i – порядковый номер тела; N – количество тел в системе.

 

 

Рис. 1. Кинематическая схема опорно-двигательного аппарата тела
человека в положении «Вис на перекладине»

 

В развернутой записи, для рассматриваемой 8-ми звенной биомеханической системы, уравнения, определяющие момент инерции системы тел относительно оси вращения О, находятся из выражения

 

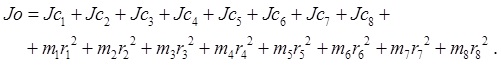                                         (2)

 

Здесь следует учесть, что r_i²  находится из выражения

 

 

Здесь r_i² – квадрат расстояния от центра масс i-го тела до оси вращения О; Xc_i² – квадрат расстояния от центра масс i-го тела до оси вращения по оси Ох; Yc_i² – квадрат расстояния от центра масс i-го тела до оси вращения по оси Оy.

Так как Xc_i, Yc_i определены в ранее выполненной лабораторной работе, то их вычисление в данном случае не обязательно, а достаточно их взять из предыдущей лабораторной работы и затем подсчитать последовательно Xc_i², Yc_i², а затем и r_i².

3. Выписать, как показано ниже в табл. 1, в качестве исходных данных значения веса каждого сегмента (лабораторная работа 1) и координату его центра масс по оси Ох и оси Оу (лабораторная работа 2).

Таблица 1

Вес сегментов (P_i), координата центра масс сегментов (Xc_i) по оси Ох и (Yc_i)
по оси Оу декартовой системы координат

 

Записать в колонку 3 табл. 1 значения веса сегмента, в колонку 5 координату центра масс сегмента по оси Ох, в колонку 7 координату центра масс сегмента по оси Оу. Так как продольная ось сегментов совпадает с осью Оу декартовой системы координат, то все координаты центра масс сегментов по оси Ох равны нулю, что и вписать в колонку 5 табл. 1. Кроме этого следует учитывать, что тело спортсмена расположено в минусовой области числовой оси Оу. Поэтому все значения координат центра масс сегментов по оси Оу (ось Ох, лабораторная работа №3) берутся со знаком «-» и записываются в колонку 7 табл. 1.

4. Вычислить массу отдельных сегментов, а результаты вычислений вписать в колонку 4 табл. 1.Формульное выражение массы i – го сегмента (m_i)  в технической системе мер и весов имеет вид

 

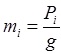.                                                                                                   (3)

 

Здесь: g – ускорение свободно падающего тела, равное 9,806 м/с².

И здесь же следует учесть, отдельные сегменты имеют парное строение и их массу необходимо удваивать (кисть, предплечье, плечо, бедро, голень, стопа).

5. Подготовить табл. 2.

Таблица 2

Биомеханические характеристики сегментов тела человека

 

В колонку 3 табл. 2 вписать карандашом значение центрального момента инерции сегментов, вычисленные в предыдущей  лабораторной работе. Далее, каждое из значений центрального момента инерции разделить на 9,806 (для перевода в техническую систему мер и весов), а затем, учитывая, что отдельные сегменты имеют парное строение и их центральный момент инерции необходимо умножить на два (кисть, предплечье, плечо, бедро, голень, стопа). После выполнения всех этих операций стереть карандашную запись и вписать ручкой величину центрального момента инерции сегмента в колонку 3 табл. 2.

6. Вычислить для каждого из сегментов квадрат расстояния от его центра масс до оси вращения (гриф перекладины) по формуле

 

r_i² = Xc_i²  + Yc_i² .

 

Данные для квадрата расстояния проекции центра масс сегмента на ось Ох (Xc_i²) и ось Оу (Yc_i²) взять из табл. 1, колонки 6 и 8 соответственно.

7. Вычислить последовательно для каждого сегмента произведение его массы на квадрат расстояния до оси вращения. Для этого надо перемножить массу сегмента (колонка 4 табл. 1) на данные колонки 4 табл. 2 (для каждой из строк табл.) и вписать полученные значения в колонку 5 табл. 2.

8. В колонке 6 табл. 2 содержатся результаты сложения данных строковых элементов колонок 3 и 5.

И на заключительном этапе выполнения лабораторной работы, в соответствии с уравнениями 1,2 необходимо результаты колонки 6 табл. 2 сложить построчно. Полученная сумма и будет являться  значением момента инерции биомеханической системы относительно оси вращения (гриф перекладины) для положения гимнаста: «Вис на перекладине».

Решение задачи 2

1. Нарисовать в декартовой системе координат кинематическую схему опорно-двигательного аппарата тела человека, в положении, соответствующим решению задачи 2 (рис. 2).

 

 

Рис. 2. Кинематическая схема опорно-двигательного аппарата тела

человека в положении «Вис углом на гимнастической стенке»

 

Ввести в схему принятые в лабораторной работе 3 соответствующие обозначения для координат центра масс сегментов.

2. Этот этап работы полностью соответствует этому же этапу работы решения первой задачи, так как уравнения по которым определяется момент инерции системы тел относительно заданной оси вращения не меняются в зависимости от изменения конфигурации биомеханической системы.

3. Выписать, как показано ниже в табл. 3, в качестве исходных данных значения веса каждого сегмента (лабораторная работа 3) и координату его центра масс по оси Ох и оси Оу (лабораторная работа 3).

Записать в колонку 3 табл. 1 значения веса сегмента, в колонку 5 координату центра масс сегмента по оси Ох, в колонку 7 координату центра масс сегмента по оси Оу. Так как продольная ось сегментов 1-4, 8 совпадает с осью Оу декартовой системы координат, то все координаты центра масс сегментов 1-4, 8 по оси Ох равны нулю, что и вписать в колонку 7 табл. 3. Продольная ось сегментов 5-7 совпадает с осью Ох декартовой системы координат, поэтому координаты центра масс сегментов 5-7 по оси Ох равны нулю, что и вписать в колонку 5 табл. 3.

Здесь следует учитывать, что координаты центра масс сегментов под номерами 1-4, 8 по оси Оу совпадают с соответствующими координатами из табл. 1 лабораторной работы №6. Для сегментов же 5, 6, 7 координата центра масс по оси Оу равна координате тазобедренного сустава (лабораторная работа №3). Координата центра масс этих сегментов по оси Ох совпадает с аналогичными координатами из второй части лабораторной работы №3.

4. Вычислить массу отдельных сегментов, а результаты вычислений вписать в колонку 4 табл. 3. Напомним, что формульное выражение массы i – го сегмента (m_i) в технической системе мер и весов имеет вид

 

.

 

Здесь g – ускорение свободно падающего тела, равное 9,806 м/с².

И здесь же следует учесть, отдельные сегменты имеют парное строение и их массу необходимо удваивать (кисть, предплечье, плечо, бедро, голень, стопа).

 

Таблица 3

Вес сегментов (P_i), координата центра масс сегментов  (Xc_i) по оси Ох и (Yc_i) по оси Оу декартовой системы координат

 

5. Подготовить табл. 4.

В колонку 3 табл. 4 вписать карандашом значение центрального момента инерции сегментов, вычисленные в предыдущей  лабораторной работе. Далее, каждое из значений центрального момента инерции разделить на 9,806 (для перевода в техническую систему мер и весов), а затем, учитывая, что отдельные сегменты имеют парное строение и их центральный момент инерции необходимо умножить на два (кисть, предплечье, плечо, бедро, голень, стопа).

Таблица 4

Биомеханические характеристики сегментов тела человека

 

После выполнения всех этих операций стереть карандашную запись и вписать ручкой величину центрального момента инерции сегмента в колонку 3 табл. 4.

6. Вычислить для каждого из сегментов квадрат расстояния от его центра масс до оси вращения (гриф перекладины) по формуле

 

r_i² = Xc_i²  + Yc_i² .

 

Данные для квадрата расстояния проекции центра масс сегмента на ось Ох (Xc_i²) и ось Оу (Yc_i²) взять из табл. 3, колонки 6 и 8 соответственно.

7. Вычислить последовательно для каждого сегмента произведение его массы на квадрат расстояния до оси вращения. Для этого надо перемножить массу сегмента (колонка 4 табл. 2) на данные колонки 4 табл. 4 (для каждой из строк таблицы) и вписать полученные значения в колонку 5 табл. 4.

8. В колонке 6 табл. 6 содержатся результаты сложения данных строковых элементов колонок 3 и 5.

И на заключительном этапе выполнения лабораторной работы, в соответствии с уравнениями 1,2 необходимо результаты колонки 6 табл. 4 сложить построчно. Полученная сумма и будет являться  значением момента инерции биомеханической системы относительно оси вращения (гриф перекладины) для положения гимнаста: «Вис углом на гимнастической стенке».