Рассмотрим возможные способы построения программного управления на кинематическом уровне. Теоретический анализ системы уравнений целенаправленных движений человека (6.15) показывает, что все возможные способы задания ограничений на обобщенные координаты биомеханической системы и их первые и вторые производные по времени можно представить в виде схемы (рис. 6.6).

 

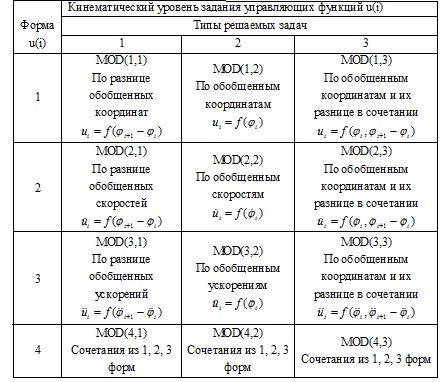
Рис. 6.6. Классификация математических моделей синтеза движений биомеханических систем по способу задания управляющих функций на кинематическом уровне формирования программного управления

 

В схеме, приведенной на рис. 6.6, отражены функциональные связи, накладываемые на определенные группы кинематических характеристик и определяющие характер задания программы движения в целом и программного управления в частности. По формам задания функциональных связей в программном управлении можно выделить 3 главные группы связей, существующих между звеньями биомеханической системы:

-   по обобщенным координатам;

-   по обобщенным скоростям;

-   по обобщенным ускорениям.

Четвертая группа связей включает всевозможные  сочетания из элементов трех главных групп: одновременно часть программных управлений представлена первой формой функциональной связи, часть – второй, оставшиеся – третьей, а также возможны разнообразные их комбинации.

Рассматриваемая классификационная схема (см. рис. 6.6) обобщает случаи и по типу решаемых задач. Дело в том, что в каждом конкретном движении используются функциональные связи программного управления, позволяющие реализовать программу движения только одного из типов решаемых задач.

Например, при синтезе упражнений в висе на перекладине можно воспользоваться любой из форм функциональной связи, относящейся к первому типу решаемых задач. При моделировании же техники схода из стойки на руках на брусьях необходимо задать программное управление для описания движения рук, т.е. воспользоваться какой-либо формой функциональной связи из 2-го типа решаемых задач. Следовательно, для синтеза конкретного двигательного действия должна быть построена своя конструктивная математическая модель синтеза целенаправленного движения, относящаяся к определенному типу решаемых задач.

Приведенная на рис. 6.6 схема охватывает все теоретически возможные формы задания программного управления на кинематическом уровне. Знание классификационной схемы математических моделей синтеза движений биомеханических систем, позволяет построить и соответствующие конструктивные модели, адекватно решающие поставленную двигательную задачу. Формально, классификационную структуру математических моделей синтеза движений биомеханических систем, можно представить в виде матричной модели MOD, элементами которой (mod_i,j) являются конструктивные математические модели. Размер матрицы MOD равен 4х3, в которой число строк i=1, 2, 3, 4; число столбцов j=1, 2, 3.