Моделирование – один из древнейших методов научного познания, широко применяющийся в архитектуре, скульптуре, технике. И, пожалуй, в настоящее время трудно назвать ту область человеческой деятельности, в которой в той или иной степени не использовались бы методы машинных экспериментов с моделями сложных систем. Особенно актуальны проблемы моделирования в сфере управления различными системами, основанными на процессах принятия решений.
В то же время, несмотря на интенсивное развитие используемых в моделировании средств и методов, некоторые частные вопросы методологии моделирования еще ждут своей разработки. Действительно, уже в самом начале анализа метода моделирования мы встречаемся с тем, что в науке пока не существует общепринятого определения понятия «модель» Например, в Советском энциклопедическом словаре (1981) дано 7 определений модели, включающих в себя и определение модели в широком смысле (с.828): «модель – любой образ (мысленный или условный: изображение, описание, схема, чертеж, график, план, карта и т.п.) к.-л. объекта, процесса или явления ("оригинала" данной м.), используемый в качестве его "заместителя", "представителя"».
Предлагаемое определение модели обладает некоторой неопределенностью, в частности, не очень ясны функции модели, на что ориентирована модель в научно-исследовательских целях и т.д. Одно из наиболее лучших определений принадлежит Б.А.Штоффу (1966), согласно которому (с. 93): «под моделью понимается такая мысленно представляемая или материально реализованная система, которая, отображая или воспроизводя объект исследования, способна замещать его так, что ее изучение дает нам новую информацию об этом объекте».
Следовательно, одна из важнейших функций модели заключается в получении новой информации об объекте исследования. Причем, эту информацию получают, изучая не сам объект познания, а его модель, которая может быть мысленной или материально реализованной. Таким образом, при моделировании между исследователем и изучаемым объектом или процессом ставится некоторое промежуточное звено – модель, т.е. моделирование, есть особая форма опосредования.
Логической основой различных видов моделирования является теория подобия, согласно которой два явления подобны, если по заданным характеристикам одного явления можно получить характеристики другого. В соответствии с этим наиболее широкое распространение получило определение моделирования, сформулированное И.Б.Новиком (1965).
Автор рассматривает моделирование как метод практического или теоретического опосредованного оперирования объектом, в ходе которого исследуется непосредственно не сам интересующий нас объект, а некоторая промежуточная вспомогательная система (естественная или искусственная), которая:
а) находится в некотором объективном соответствии с познаваемым объектом;
б) обладает возможностью на известных этапах исследования замещать в определенных отношениях изучаемый объект;
в) реализует необходимость давать в процессе исследования качественную и количественную информацию об интересующем нас объекте.
Сама эта промежуточная вспомогательная система (модель) может выступать в виде естественной, искусственной, знаковой системы.
В качестве основных, характерных черт модели предложено считать:
1. Объективное соответствие с моделируемым объектом.
2. Способность замещать познаваемый объект на определенных этапах исследования.
3. Возможность давать в ходе исследования необходимую информацию, допускающую опытную проверку.
4. Наличие четких правил перехода от модельной информации к информации о самом моделируемом объекте.
Как уже отмечалось, в основе моделирования лежит теория подобия, утверждающая, что абсолютное подобие возможно лишь при замене одного моделируемого объекта другим точно таким же. Так как абсолютного подобия достичь практически невозможно, то в исследованиях обычно стремятся к тому, чтобы модель достаточно хорошо и полно отражала исследуемую область функционирования моделируемого объекта или процесса. Поэтому в качестве одного из признаков классификации моделей и моделирования можно выбрать признак полноты модели и в соответствии с ним выделить следующий класс моделей: полные, неполные, приближенные.
Классификация моделей на полные, неполные и приближенные не несет той методологической нагрузки, которая позволила бы определить общую направленность моделируемого процесса в плане его содержательной и конструктивной сущности. По мере конкретизации модели она из приближенной приобретает черты неполной и в окончательном варианте формируется в полную модель, описывая один и тот же моделируемый процесс. А это – конструктивные этапы построения модели, раскрывающие последовательность получения более полной информации об объекте исследования.
Существенно большей классификационной общностью обладает способ дифференцирования моделей, предложенный Б.Я. Советовым и С.А.Яковлевым (1985) (рис. 6.1). По мнению авторов, модели можно классифицировать в зависимости от условий, характера изучаемых процессов в моделируемой системе и формы представления объектов моделирования. Предлагаемая классификация достаточно логично и системно объединяет различные виды моделирования и охватывает широкий спектр моделируемых процессов, объектов и явлений.
По условиям и характеру изучаемых процессов в системе, авторы классификационной схемы (см. рис. 6.1), выделяют следующие виды моделирования:
1. Детерминированное моделирование – отображает причинно-следственные связи и процессы, в которых отсутствуют любые случайные воздействия.
2. Стохастическое моделирование – отображает вероятностные процессы и события.
3. Статическое моделирование – описывает поведение объекта в какой-либо момент времени.
4. Динамическое моделирование – отражает эволюцию исследуемого объекта во времени.
5. Дискретное моделирование – служит для описания процессов, которые предполагаются дискретными.
6. Непрерывное моделирование – отражает непрерывные процессы в системах.
7. Дискретно-непрерывное моделирование – используется для описания дискретных и непрерывных процессов в изучаемой системе.
![Классификация видов моделирования [по Советову Б.Я., Яковлеву С.А. (1985)] рис 6.1](img/image/6.1.jpg)
Рис. 6.1. Классификация видов моделирования
[по Советову Б.Я., Яковлеву С.А. (1985)]
В зависимости от формы представления моделируемого объекта выделяют два вида моделирования:
1. Мысленное моделирование – применятся к объектам, существующим вне условий их физического создания или не реализуемых в заданных интервалах времени.
2. Реальное моделирование – используется возможность исследования различных характеристик функционирования системы или на реальном объекте, или на его части.
Мысленное моделирование реализуется в трех формах его проявления:
1. Наглядное моделирование – осуществляется на базе представлений человека о реальных объектах в форме наглядных моделей, отображающих явления и процессы, протекающие в исследуемой системе, и включает в себя три вида моделирования – гипотетическое, аналоговое и макетирование:
- гипотетическое моделирование – исследователем закладывается некоторая гипотеза о закономерностях функционирования исследуемого реального объекта, базирующаяся на знании причинно-следственных связей изучаемой системы на входе и выходе;
- аналоговое моделирование – основывается на использовании аналогий различного уровня, отражающих соответственно только одну или несколько сторон функционирования моделируемой системы;
- макетирование – в основе создания мысленных макетов также лежат аналогии, базирующиеся на причинно-следственных связях процессов и явлений моделируемой системы.
2. Символическое моделирование – основано на условном обозначении отдельных понятий:
- знаковое моделирование – с помощью условных обозначений отдельных понятий (знаков) и аппарата теории множеств составляются цепочки слов и предложений;
- языковое моделирование – в основе лежит некоторый тезаурус предметной области исследования, исключающий неоднозначность понятий.
3. Математическое моделирование – процесс установления соответствия реальному объекту математического объекта, называемого математической моделью. Выделяют три вида математического моделирования:
- аналитическое моделирование – процессы функционирования элементов системы и системы в целом записываются в форме функциональных соотношений (алгебраических, интегро-дифференциальных, конечно-разностных);
- имитационное моделирование – моделирующий алгоритм воспроизводит процесс функционирования исследуемой системы во времени, что позволяет по исходным данным получать информацию о состоянии процесса в определенные моменты времени. В настоящее время имитационное моделирование – наиболее эффективный, а часто и единственный, практически доступный метод исследования больших систем. Имитационное моделирование на ЭВМ положено в основу структурного, алгоритмического и параметрического синтеза больших систем, которые являются оптимальными по некоторым критериям оценки эффективности;
- комбинированное моделирование – (аналитико-имитационное) объединяет достоинства аналитического и имитационного моделирования.
Реальное моделирование объединяет два вида моделирования:
1. Натурное моделирование – проведение исследований на реальном объекте для выявления закономерностей протекания реального процесса. Существует три разновидности натурного моделирования: научный эксперимент, комплексные испытания, производственный эксперимент:
- научный эксперимент – широкое использование средств автоматизации проведения эксперимента с возможностью вмешательства исследователя в процесс исследования;
- комплексные испытания – выявление общих закономерностей надежности промышленных изделий методом повторения испытаний;
- производственный эксперимент – обобщение опыта, накопленного в ходе производственного процесса с использованием статистического материала.
2. Физическое моделирование – в отличие от натурного осуществляется на специальных установках, воспроизводящих природу явлений в двух масштабах времени:
- реальном;
- нереальном – исследуются так называемые «замороженные» процессы, фиксируемые в некоторый момент времени.
Рассматривая модель в плане выполняемых ею функций, можно отметить, что для любой модели задачи исследования делятся на два класса: задачи анализа и синтеза. При этом под анализом понимается описание свойств элементов системы на основании информации об ее характеристиках в зависимости от определяющих параметров и структуры системы. Задача же синтеза заключается в получении информации об определяющих параметрах и (или) структуры системы по заданному набору требуемых свойств. То есть, в известном смысле, задача синтеза – задача обратная задаче анализа. В связи с этим конкретизируем задачи биомеханического исследования технических действий спортсмена в плане их единообразной постановки и трактовки с системных позиций.
Во-первых, среди обширного круга задач по биомеханике технических действий спортсмена, можно отметить тематическую общность направленности биомеханических исследований: в виде исследований двигательных действий на кинематическом и динамическом уровнях.
Во-вторых, для каждой из групп задач кинематического или динамического уровней возможны две противоположные постановки задачи: обратная – задача анализа и прямая – задача синтеза. Следовательно, с достаточно большой степенью общности большинство задач биомеханики движений человека можно дифференцировать на четыре группы задач по двум типам и классам (рис. 6.2).
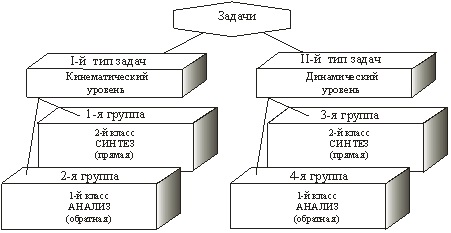
Рис. 6.2. Классификация задач биомеханики движений человека
Первый класс задач решается с помощью расчетных моделей анализа движений биомеханических систем, второй – с использованием математических моделей синтеза движений биомеханических систем.