Изменение позы спортсмена в полетной части упражнения может привести к различным последствиям, которые определяются величиной начального вращательного импульса. Под начальным вращательным импульсом понимается величина кинетического момента (К) биомеханической системы, который для тела в безопорном состоянии определяется зависимостью
K = J. (5.1)
Здесь J – величина момента инерции тела относительно оси, проходящей через его центр масс; – угловая скорость тела.
Для биомеханической системы величина кинетического момента определяется суммой кинетических моментов его отдельных звеньев. Например, для трехзвенной модели биомеханической системы (в которой руки – первое звено, туловище с головой – второе звено, ноги – третье звено) кинетический момент всей системы (К) равен
К = К1 + К2 + К3. (5.2)
Следует помнить, что в полетной части упражнения осью вращения является ось, проходящая через общий центр масс биомеханической системы.
Рассмотрим следующий пример: батутист совершает прыжки на батуте.
В крайней верхней точке вылета вверх спортсмен, по заданию тренера, должен выполнить двигательное задание: совершить сгибание ног в тазобедренных суставах до угла между ногами и туловищем в 90О. Необходимо определить: в каком положении окажутся звенья тела спортсмена после выполнения поставленного двигательного задания?
При решении данной задачи будем исходить из следующего положения: в полетной части упражнения величина кинетического момента биомеханической системы не изменяется. Сущность данного положения сводится к тому, что в безопорном состоянии величина кинетического момента тела спортсмена является константой и определяется начальными условиями движения.
За основу возьмем несколько возможных конечных положения звеньев тела спортсмена, являющихся результатом решения поставленной двигательной задачи:
1. Предположим, что в конечном положении руки и туловище батутиста остаются на месте, занимая вертикальное положение, а ноги принимают горизонтальное положение (рис. 5.1, II). Возможно также и вращательное движение всей биомеханической системы по сальто назад (рис. 5.1, III).
2. Аналогично, ноги в конечном положении остаются на месте, а туловище и руки, вращаясь вперед, приходят в горизонтальное положение (рис. 5.1, IY). Можно также рассматривать и вращательное движение спортсмена по сальто вперед (рис. 5.1, Y).
3. Руки и туловище совершают поворот навстречу движению ног и в конечном положении и ноги и туловище с руками отклоняются от исходного вертикального положения на 45О (рис. 5.1, YI).
Биомеханический анализ возможных положений построим на законе сохранения кинетического момента биомеханической системы в полетной части упражнений. Заметим, что в исходном положении, перед началом выполнения двигательного задания все звенья тела имели нулевую угловую скорость. Поэтому, исходный кинетический момент биосистемы был равен нулю.
Первое конечное положение (рис. 5.1, II) для нас неприемлемо, так в этом случае, в результате вращения ног, ноги приобретают вращательный импульс, и кинетический момент всей биосистемы не будет равен нулю (первоначально имеющемуся). Тем более, биомеханически необоснованным является вращение спортсмена по сальто назад (рис. 5.1, III), так как в этом случае вращательный импульс приобретают все звенья тела спортсмена – закон сохранения кинетического момента нарушается.
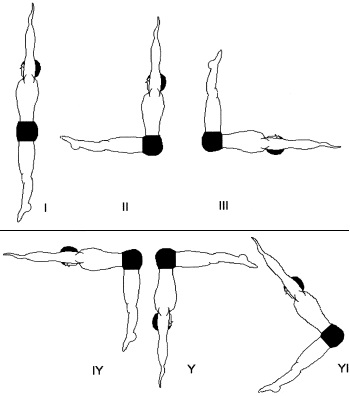
Рис. 5.1. Возможные положения батутиста после выполнения
двигательного задания
По этим же соображениям неприемлемым являются четвертое и пятое конечные положения батутиста (рис. 5.1, IY, Y), так как в результате вращения туловища и рук они приобретают определенную величину кинетического момента, и кинетический момент всей биомеханической системы в конечном положении будет отличаться от нуля.
Реальному движению будет соответствовать шестое анализируемое положение (рис. 5.1, YI). Действительно, при движении туловища и рук навстречу ногам, как ноги, так и туловище с руками приобретают определенную величину кинетического момента. Но, учитывая, что кинетический момент – векторная величина (имеет модуль и направление), то алгебраическая сумма положительного и отрицательного значения кинетического моментов ног и туловища с руками останется по-прежнему равной нулю. Закон сохранения кинетического момента не нарушен.
В заключение остается отметить, что угол поворота звеньев тела спортсмена будет определяться величиной их момента инерции: чем больше момент инерции, тем на меньший угол совершается поворот. Например, допустим, что при выполнении вышерассмотренного двигательного задания, момент инерции туловища, головы и рук в два раза больше момента инерции ног спортсмена. В этом случае первая биокинематическая цепь совершает поворот на 30О, а ноги – на 60О. И, наоборот: если момент инерции ног в два раза больше момента инерции туловища, головы и рук, то в этом случае ноги совершают поворот на 30О, а туловище, голова и руки – на 60О.
Следовательно, для рассматриваемой биомеханической закономерности зависимость обратная: во сколько раз момент инерции туловища, головы и рук больше момента инерции ног во столько раз меньше и угол поворота первой биокинематической цепи по отношению к ногам. И наоборот.
Таким образом, при выполнении спортсменом сгибательных движений в суставах в полетной части упражнений звенья тела совершают противонаправленные повороты на величину угла, определяемого обратной зависимостью соотношения их моментов инерции.
Данную закономерность следует учитывать в педагогическом процессе. Например, допустим, что тренер при объяснении техники сальто назад с места в группировке поясняет занимающемуся, что для выполнения упражнения необходимо выпрыгнуть как можно выше вверх и в крайнем верхнем положении резко подтянуть ноги к плечам. Несомненно, данная трактовка техники выполнения упражнения является методической ошибкой, так как не только ноги будут совершать вращение к плечам, но и плечи, в свою очередь будут двигаться к ногам.