Кинематические характеристики, определяя геометрию движения, не учитывают движущиеся массы и действующие силы и поэтому не в состоянии дать ответ на вопрос о причинах возникновения и изменения движений. Причины возникновения и изменения движений раскрывает динамика с использованием динамических характеристик, включающих в себя, так же, как и кинематические характеристики, три большие группы характеристик (рис. 4.20):

1)      силовые;

2)      инерционные;

3)      энергетические.

Непосредственно к основным силовым характеристикам относятся:

1.  Сила – мера механического воздействия одного тела на другое в данный момент времени в поступательных движениях.

2.  Момент силы – мера вращающего действия силы на тело. Момент силы определяется произведением силы на ее плечо. Плечо силы – перпендикуляр, восстановленный от оси вращения на линию действия силы.

3.  Сила реакции опоры – мера противодействия опоры при действии на нее тела, находящегося с ней в контакте (в покое – статическая или в движении – динамическая).

4.  Сила действия среды – мера действия внешней среды на тело (выталкивающая сила, подъемная сила, сила трения, сила сопротивления внешней среды).

 

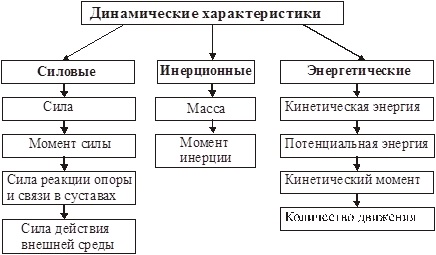
Рис.4.20. Классификация динамических характеристик двигательных действий

 

К основным инерционным характеристикам относятся:

-     Момент инерции – мера инертности тела во вращательном движении. Численно момент инерции равен сумме произведений масс всех частиц тела на квадрат расстояния каждой частицы до оси вращения.

-     Масса – мера инертности тела при поступательном движении. Она измеряется отношением приложенной силы к вызываемому силой ускорению.

Основные энергетические характеристики:

1. Кинетическая энергия – энергия движущегося тела (энергия движения). Кинетическая энергия может трансформироваться в потенциальную энергию. При поступательном движении кинетическая энергия определяется половиной произведения массы тела и квадрата его линейной скорости. В сложном движении при определении кинетической энергии (Т) учитывается и вращательная составляющая движущегося тела

                                                                                                        (4.74)

Таким образом, кинетическая энергия будет определяться суммой кинетических энергий поступательного и вращательного движения. Для вращательной компоненты движения кинетическая энергия определяется половиной произведения момента инерции и его угловой скорости.

Движение биомеханической системы является сложным движением, так как оно включает в себя поступательную и вращательную компоненты, соотносимые к каждому звену рассматриваемой модели. Действительно, в процессе выполнения спортсменом различных упражнений как центр масс каждого сегмента (звена) совершает поступательное движение относительно внешней системы отсчета, так и каждый сегмент (звено) совершает вращательное движение, одной из характеристик которого является угловая скорость. Поэтому, в соответствии с выражением (4.74), кинетическую энергию для первого звена трехзвенной модели запишем в виде

 

                                                                                              (4.75)

 

где

– линейная скорость центра масс первого звена по оси Ох декартовой системы координат;

 – линейная скорость центра масс первого звена по оси Оу декартовой системы координат;

 – угловая скорость первого звена;

J ₁ – центральный момент инерции первого звена;

m₁ – масса первого звена;

T₁ – кинетическая энергия первого звена.

Оставив принятые обозначения и введя для второго звена цифровой индекс 2, получим уравнение кинетической энергии для второго звена в виде

 

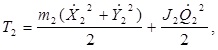                                                                                    (4.76)

 

И, аналогичным образом, для третьего звена имеем

 

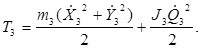                                                                                       (4.77)

 

Выполним дальнейшие преобразования. Заменим линейные скорости центров масс звеньев тела на их выражения через обобщенные скорости и длины звеньев тела. Получим:

для первого звена 

                                                              

 

 

для второго звена  

                                                             

 

для третьего звена                  

                                           

 

 

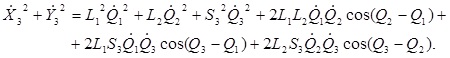
Подставим полученные выражения в уравнения (4.75), (4.76), (4.77). Окончательно имеем

 

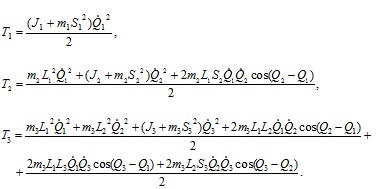                                                (4.78)

 

Полученные уравнения определяют величину кинетической энергии звеньев тела человека и для численного решения в правых частях уравнений достаточно знать количественные значения динамических характеристик звеньев тела и обобщенных координат. Так как кинетическая энергия системы тел равна сумме кинетических энергий отдельных тел, то можно записать

 

 

где Т - кинетическая энергия трехзвенной биомеханической системы.

Не прибегая к подробным выкладкам, запишем уравнение кинетической энергии в окончательном виде:

 

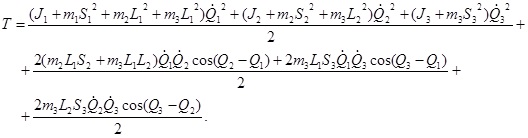
Обозначим через коэффициенты  масс-инерционные характеристики звеньев тела

 

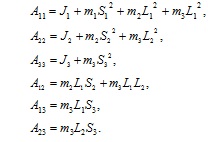
В этом случае выражение кинетической энергии для трехзвенной биомеханической системы можно записать в следующей форме:

 

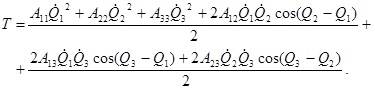                                                           (4.79)

Для N-звенной биомеханической системы кинетическая энергия в компактной записи имеет вид

 

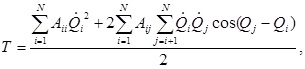                                                                   (4.80)

 

а для i-го звена, в виде удобном для программирования на ЭВМ, получим

 

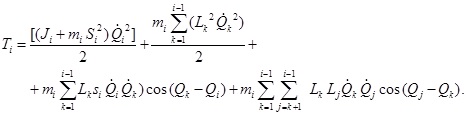                                         (4.81)

Уравнения (4.80), (4.81) позволяют написать выражение кинетической энергии звеньев тела и биомеханической системы для N-звенной модели, состоящей практически из любого количества звеньев, в развернутом виде. Это позволяет, не зная явный вид уравнений кинетической энергии i-го звена, вычислять искомые значения, по стандартной программе, составленной для алгоритмов (4.80), (4.81).

2. Потенциальная энергия – энергия покоя. Потенциальная энергия (П) определяется произведением веса тела (P) и расстоянием до опоры (H) по вертикали

П = РH.                                                                                                        (4.82)

 

Потенциальная энергия может переходить в кинетическую энергию, что объясняет увеличение скорости движущегося тела во вращательном движении в условиях опоры (при перемещении из опорного положения в вис).

3. Кинетический момент – мера вращательного движения тела. Кинетический момент (K) измеряется произведением момента инерции тела (J) и угловой скорости ()

 

  .                                                                                                     (4.83)

 

Момент инерции определяется относительно оси вращения. Поэтому:

-     осью вращения тела в условиях опоры является место контакта тела с опорой;

-     в безопорном положении осью вращения тела является общий центр масс тела.

В полетной части упражнения кинетический момент – величина постоянная. Применительно к биомеханической системе это означает, что любые сгибательно-разгибательные движения спортсмена в суставах в полетной части упражнения, изменяющие конфигурацию биосистемы, не способны изменить величину его кинетического момента относительно оси вращения проходящей через общий центр масс биомеханической системы.

4. Количество движения – мера поступательного движения тела. Количество движения (Q) определяется произведением массы тела (m) и его линейной скорости ()

 

.                                                                                                     (4.84)

 

Количество движения – аналог кинетического момента в поступательном движении. Если во вращательном движении меру инертности тела характеризует момент инерции (J), то в поступательном движении – масса (m). И, если во вращательном движении кинетический момент определяется как произведение момента инерции тела на его угловую скорость, то в поступательном движении количество движения зависит от величины линейной скорости.