В последние десятилетия XX века такое понятие, как детерминированный хаос прочно вошло в характеристику эволюционного поведения объектов и систем, движение которых казалось бы полностью детерминировано, т.е. однозначно определено во времени динамическими законами.

Определение 8.2. Математическая модель, описывающая состояние реальной системы, называется детерминированной, если существует правило в виде дифференциальных или других уравнений, однозначно определяющее состояние системы в любой момент времени, исходя из заданных начальных условий,

q(t) = Ф(q₀, t),   q₀ = q(t₀) ,

где q={q₁, q₂, …, q_m} – вектор состояния системы.

Хаос означает состояние беспорядка или нерегулярности. Естественно предположить, что поведение детерминированной системы достаточно регулярно и далеко от хаотичности, поскольку последовательные состояния непрерывно развиваются одно из другого. Но ещё Пуанкаре (1882 г.) открыл, что в детерминированных механических системах, эволюция которых во времени определяется уравнениями Гамильтона, может появляться в некоторых случаях хаотическое движение. Многими физиками это было воспринято как курьёз, и прошло около 70 лет, пока метеоролог Е.Н. Лоренц (1963 г.) не обнаружил, что даже простая система из трёх связанных нелинейных дифференциальных уравнений первого порядка может привести к совершенно хаотическим траекториям. Фактически Лоренц открыл один из первых примеров детерминированного хаоса. И хотя эта работа также долго оставалась малоизвестной, в настоящее время её значимость является общепризнанной.

Определение 8.3. Под детерминированным хаосом подразумевается нерегулярное или хаотическое движение, порождённое нелинейными системами, для которых динамические законы однозначно определяют эволюцию состояния системы во времени при известных начальных условиях. (Или кратко: система детерминирована, а её поведение может быть хаотичным).

Итак, оказалось, что для детерминированных систем существует «горизонт» предсказуемости. И трудности здесь не технические, которые можно обойти, создав более мощный компьютер, а принципиальные. Это такое же серьёзное препятствие, как, например, существование максимальной скорости передачи сигналов или невозможность создания вечного двигателя. Попытка брать «числом» (длиной числа), а не умением тут не проходит. Такие системы обладают внутренней неустойчивостью, которая, однако, не разрушает их, а приводит к сложному поведению с ограниченной предсказуемостью.

Таким образом, становится практически невозможно предсказать длительное поведение таких систем, поскольку реально начальные условия можно задать только с конечной точностью, а ошибки иррациональных чисел, заданных конечным числом цифр, экспоненциально нарастают. Т.е. понятие хаоса непосредственно связанно с известным в математике явлениемчувствительности к начальным условиям. Лоренц назвал эту чувствительность эффектом бабочки, поскольку решение его уравнений, описывающих приближенно потоки воздуха в атмосфере Земли, может изменить взмах крыльев бабочки.

Для описания таких ситуаций пришлось ввести новый класс моделей – динамические системы с джокерами. Напомним, что в карточных играх джокер (от английского слова joker – шутник) может быть назначен любой картой по желанию того, кому он достался. Это резко повышает неопределённость ситуации.

Рассмотрим обычное фазовое пространство, в котором, однако, есть маленькая область G2, которую называют областью джокера, а всё остальное – область G1 (рис. 8.1).

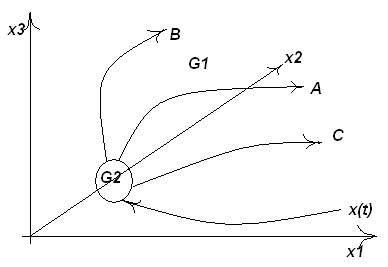
Рис. 8.1

Когда точка, соответствующая положению нашей системы, находится в области G1, все происходит как всегда: будущее однозначно определяется прошлым.

Но, допустим, траектория подошла к области G2. Тут в дело вступает джокер. Так разработчики таких моделей назвали правило, которое определяет дальнейшее. В соответствии с ним система может совершать скачек. Джокеры бывают разные.

Джокер первого рода скачком перебрасывает нашу систему из области джокера G2 в некую точку А.

Джокер второго рода действует хитроумнее: с вероятностью р₁ он переводит систему в точку В, с вероятностью р₂ – в точку С.

Джокер третьего рода ещё коварнее. Он может перевести наш объект в любую точку пространства, но с разной вероятностью.

Таким образом, в фазовом пространстве многих объектов, с которыми мы имеем дело, есть места, называемые областями джокеров, в которых случайность, или игровой элемент, либо фактор, не имеющий никакого значения в другой ситуации, может оказаться решающим, и не только повлиять на судьбу системы, но и скачком перевести ее в другую точку фазового пространства. Правило, по которому совершается этот скачок, и называется джокером.

Джокеры начали свою жизнь в науке в конце 90-х годов ХХ века (1997 г.), но уже нашлось много задач, где их применение оказалось полезным: в различных экспертных системах, в технологии принятия крупных решений, на финансовых рынках.