|
Тема. Решение задач по теме "Магнитное поле в вакууме". Цели: - углубить и закрепить понятия об индукции магнитного поля, силе Ампера, силе Лоренца; - показать на нескольких примерах методы решения задач на движение заряженных частиц в магнитном поле. Ход занятия В ходе проведения занятия необходимо рассмотреть ряд качественных задач и далее решить несколько расчетных задач по мере возрастания их сложности. При решении задач на действие магнитного поля на заряды и проводники с током, нужно на рисунке указать направление скорости заряда или направление тока, направления вектора магнитной индукции и сил Лоренца или Ампера. Если проводник или заряд находятся в равновесии, записать уравнение, определяющее условия равновесия. Если проводник или заряд движутся, записать уравнение движения с учетом всех действующих сил со стороны магнитного и электрического полей. Качественные задачи 1. Шнур настольной лампы, питаемой постоянным током, поднесли к магнитной стрелке. Окажет ли магнитное поле тока действие на стрелку? 
2. В сосуде с маслом имеются поплавки с магнитными стрелками. Как расположатся стрелки, если сосуд поместить внутрь кольцевого провода с током, расположенного в вертикальной плоскости? Направление тока указано на рис. 1 
3. К вершинам А и В проволочного параллелограмма (рис. 2) подведены провода от источника постоянного тока. Какова индукция магнитного поля в центре параллелограмма (точка О)? Как будет направлен вектор индукции в точке О, если ветвь параллелограмма АСВ сделать из медной, а ветвь ADB - из алюминиевой проволоки того же сечения? 
4. Дан каркас из однородной проволоки в форме куба (рис. 3) К противоположным концам диагонали подводится постоянное напряжение. По ребрам куба текут токи. Чему равна индукция магнитного поля в центре куба? 5. Какова разница в отклонении одним и тем же магнитным полем токов в ионизированном газе: а) ионов положительных и отрицательных; б) заряженных однократно, двукратно и т.д.; в) ионов с большим и малым молекулярным весом? 6. Чему равна работа силы, действующей на заряженную частицу, движущуюся в однородном магнитном поле? 7. Почему уменьшается поперечное сечение струи расплавленного металла, если по нему пропустить ток? 8. Как взаимодействуют воздушные провода, питающие движение троллейбуса? 
9. Укажите направление сил Ампера, действующих на проводник с током (рис. 4). Ответ обоснуйте. 10. Почему замкнутый подвижный проводник, по которому идет ток, стремится принять форму кольца, даже если он не находится в магнитном поле? 
11. Две стеклянные U-образные трубки (рис. 5), наполненные ртутью, соединены отрезком толстой алюминиевой проволоки. Как должны быть расположены полюсы сильного постоянного магнита, чтобы при замыкании цепи алюминиевая проволока взлетела вверх? 
12. В горизонтальной плоскости лежит подвижный виток из гибкой проволоки (рис. 6). Однородное магнитное поле направлено вниз. Как будут направлены силы, действующие на элементы витка, если по нему пропустить ток в направлении, указанном стрелкой? В обратном направлении? Какую форму примет виток в каждом случае? Что произойдет, если при заданном направлении тока изменить на противоположное направление вектора магнитной индукции? Примеры решения расчетных задач 
Задача 1. Определите, какую максимальную скорость разовьет положительно заряженное тело, скользящее по наклонной плоскости в магнитном поле с индукцией В и в поле силы тяжести. Масса и заряд тела m и q. Вектор индукции магнитного поля параллелен наклонной плоскости и перпендикулярен силе тяжести. Угол наклона плоскости к горизонту Решение: В начальный момент времени на тело действуют сила тяжести 
Тело движется с ускорением, то есть скорость его растет, а значит, растет и величина силы Лоренца. Уравнение движения тела имеет вид:
Спроецируем уравнение движения на систему координат XY (ось Х направлена вдоль наклонной плоскости, ось Y ей перпендикулярна).
Учтем, что сила трения скольжения
Из первого уравнения системы уравнений (1) видно, что скорость тела достигнет максимального значения при условии, что
Величину N можно выразить из второго уравнения в системе (2).
Видно, что с ростом скорости растет и величина силы нормальной реакции, а значит и силы трения. Скорость достигнет максимального значения при условии
Отсюда получаем следующее значение максимальной скорости:
Ответ: Задача 2. Частица, имеющая заряд электрона, влетает в однородное поле под углом Решение: 
На частицу, движущуюся в магнитном поле, будет действовать сила Лоренца
Составляющая Движение частицы по окружности будет описываться уравнением
Подставляя значение
Шаг винтовой линии равен
где Т - период движения частицы по окружности. Сила Лоренца всегда перпендикулярна скорости частицы, поэтому при движении частицы она работы не совершает, следовательно, частица будет двигаться по окружности с постоянной по модулю скоростью. Период обращения частицы по окружности будет равен
Подставим значение
Отсюда радиус окружности, по которой движется частица, определится как
Подставляя значение R в (3), получим для скорости частицы следующее выражение:
Тогда импульс частицы будет равен
Ответ: 
Задача 3. По обмотке длинного цилиндрического соленоида радиуса r протекает постоянный ток, создающий внутри соленоида однородное магнитное поле с индукцией Решение: На электрон, влетевший в магнитное поле, будет действовать сила Лоренца, направленная перпендикулярно векторам скорости электрона и индукции магнитного поля, то есть вектор силы Лоренца в любой момент времени будет лежать в плоскости, перпендикулярной оси соленоида. Скорость электрона перпендикулярна индукции магнитного поля, поэтому величина силы Лоренца будет равна Электрон внутри соленоида будет двигаться по дуге окружности. Радиус этой окружности R можно найти из уравнения движения электрона:
Отсюда
На рис. 11 показана траектория движения электрона внутри соленоида. В точке О1 находится центр окружности, описываемой электроном,
где S - длина дуги СD (путь, пройденный электроном). Поскольку
Угол
Таким образом, время движения электрона внутри соленоида будет равно
Ответ: Задача 4. Круглая металлическая пластина падает вертикально вниз в однородном магнитном поле, параллельном поверхности Земли. В процессе падения она остается параллельной линиям индукции магнитного поля и перпендикулярной поверхности Земли. Толщина пластинки d много меньше ее радиуса R, масса пластины равна m, модуль индукции магнитного поля В. Определите ускорение, с которым падает пластина. Решение: 
Предположим, что пластина падает с постоянной скоростью v. На каждый электрон будет действовать сила Лоренца F = qvB (q - заряд электрона). Пусть вектор qvB = qE где Е - напряженность электрического поля. Поскольку появится электрическое поле, напряженность которого E = Bv, то между плоскостями, ограничивающими пластину, возникнет разность потенциалов:
Пластину с разделившимися зарядами можно рассматривать как плоский конденсатор, на пластинах которого находится заряд.
где S - площадь пластин ( S =
где а - ускорение, с которым движется пластина. Таким образом, движущуюся пластину можно рассматривать как проводник с током, движущийся в магнитном поле. На такой проводник будет действовать сила Ампера.
В рассматриваемом случае сила Ампера направлена вверх. Уравнение движения пластины можно записать следующим образом:
Проецируя это уравнение на вертикальную ось Х и подставляя значение силы Ампера (6), получим:
Отсюда для ускорения, с которым движется пластина, получим следующую формулу:
Ответ: 
Задача 5. Проводящий стержень подвешен горизонтально на двух легких проводах в магнитном поле, индукция которого направлена вертикально вниз и по модулю равна В. Длина стержня L, масса провода m, длина провода l (рис. 13). К точкам закрепления проводов подключают конденсатор емкостью С, заряженный до напряжения U. Определить максимальный угол отклонения системы от положения равновесия после разрядки конденсатора, считая, что разрядка происходит за очень малое время. Решение: При подключении конденсатора по стержню потечет ток. Поскольку стержень находится в магнитном поле, на него будет действовать сила Ампера, направленная перпендикулярно стержню и вектору
Так как время разрядки мало, то можно считать, что мало и происходящее за это время отклонение стержня от положения равновесия. Кроме того, ток разрядки меняется со временем, значит, будет меняться и сила Ампера. Разобьем время разрядки на малые промежутки
где
Чтобы найти полное изменение импульса, нужно произвести суммирование по всем малым промежуткам времени.
Так как за время разрядки стержень не успевает отклониться от положения равновесия, в (7) можно перейти к скалярному суммированию:
Здесь
где q - заряд конденсатора (q = CU ). Таким образом, при разрядке конденсатора стержень приобретает скорость
Следовательно, сразу после разрядки конденсатора стержень будет обладать кинетической энергией
Так как в системе отсутствуют непотенциальные силы, этот запас кинетической энергии будет израсходован на изменение потенциальной энергии стержня в поле тяготения Земли при отклонении стержня от положения равновесия. Будем отсчитывать потенциальную энергию стержня от положения равновесия стержня, тогда
где h - высота, на которую поднимается центр масс стержня. Из рис. 14 видно, что
где
Отсюда угол отклонения
Ответ: 
Задача 6. Медный провод сечением S, согнутый в виде трех сторон квадрата, прикреплен своими концами к горизонтальной оси, вокруг которой он может свободно вращаться в однородном магнитном поле с индукцией Решение: 
Контур может совершать вращательное движение вокруг оси OO'. Вращающий момент обеспечивают силы тяжести, приложенные к каждой стороне контура и сила Ампера FA = IBl, приложенная к горизонтальной стороне (рис. 16), где l - длина стороны квадрата. Поскольку отклонившаяся от положения рамка неподвижна, алгебраическая сумма моментов всех сил, действующих на рамку, равна нулю. Моменты сил тяжести вращают рамку по часовой стрелке, а момент силы Ампера - против часовой стрелки. Поэтому моментам этих сил следует приписать разные знаки. Результирующий момент сил тяжести относительно оси OO', приложенный к сторонам квадрата, будет равен (рис. 17)
где m - масса одной стороны рамки. 
Момент силы Ампера относительно оси OO' будет равен
Силы Ампера, приложенные к вертикальным сторонам рамки, направлены в противоположные стороны и параллельны оси OO'. Эти силы растягивают рамку, а их момент относительно оси OO' равен нулю. Таким образом, условие равновесия отклонившейся в магнитном поле рамки имеет следующий вид:
Масса каждой стороны рамки равна
Ответ: Задачи для самостоятельной работы 1. В однородном постоянном во времени магнитном поле, индукция которого направлена вертикально вверх, движется подвешенный на нерастяжимой нити длины l маленький заряженный шарик. Масса шарика равна m, заряд q, период обращения Т. Найдите радиус окружности, по которой движется шарик, если нить все время натянута. Ответ: 2. Проволочная прямоугольная рамка со сторонами, массы которых равны m1 и m2, может свободно вращаться вокруг горизонтальной оси так, что одна из сторон длиной l остается неподвижной. Рамка находится в вертикальном однородном магнитном поле индукции В. Найдите такую силу тока в рамке, при которой она будет неподвижна в поле тяготения Земли и наклонена к горизонту под углом Ответ: 
3. Ответ: 4. Электрон, прошедший разность потенциалов U = 1000 В, влетает в однородное магнитное поле перпендикулярно силовым линиям магнитной индукции. Как только электрон совершает в магнитном поле четверть оборота, магнитное поле отключают, а электрон попадает в плоский заряженный конденсатор, так что его скорость направлена перпендикулярно силовым линиям электрического поля. Если длина пластин конденсатора l = 50 см, то сколько времени электрон будет двигаться между пластинами? Заряд электрона q = 1,6 Ответ: 5. Электрон с начальной скоростью V0 = 106 м/с влетает в однородное электрическое поле напряженностью Е = 100 В/м перпендикулярно силовым линиям поля. Через время t = 10-6 с электрическое поле выключают и включают однородное магнитное поле индукцией B = 10-4 Тл, силовые линии которого перпендикулярны вектору скорости электрона. Определите радиус R окружности, по которой будет двигаться электрон в магнитном поле. Заряд электрона q = 1,6 Ответ: 
6. Заряженная частица движется в однородных взаимно перпендикулярных электрическом и магнитном полях. В некоторый момент времени скорость частицы Ответ: 7. В однородном магнитном поле по горизонтальной идеально гладкой поверхности движется с ускорением а = 1 м/с2 прямолинейный проводник с поперечным сечением S = 1 мм2. По проводнику протекает ток I = 2 A. Плотность материала проводника Ответ: Рекомендуемая литература 1. Бутиков Е.И., Кондратьев А.С. Физика. Т. 2. Элетродинамика. - М.: Физматлит: Лаборатория базовых знаний; СПб.: Невский диалект, 2001. - С. 11-82. 2. Белолипецкий С.Н., Еркович О.С., Казаковцева В.А. и др. Задачник по физике. - М.: Физматлит, 2005. - С. 142-150. 3. Готовцев В.В. Лучшие задачи по электричеству. - М.; Ростов н/Д: Издательский центр "Март", 2004. - С. 117-125. |
(рис. 7). Коэффициент трения тела о плоскость равен 
.
, сила нормальной реакции опоры 
и сила трения 
тр, под действием которых тело придет в движение. Так как тело заряжено, то на него со стороны магнитного поля начнет действовать сила Лоренца, перпендикулярная векторам скорости и магнитной индукции (рис. 8). Поскольку вектор скорости тела перпендикулярен вектору магнитной индукции 
, величина силы Лоренца будет равна 
(1)
. Подставим в систему уравнений (1) величину силы трения и силы Лоренца:
(2)
, где 
- составляющую, перпендикулярную вектору индукции магнитного поля, 
- составляющую, параллельную вектору индукции магнитного поля (рис. 9). 
, получим:
(3)
(4)
и Т в (4), тогда получим:
(рис. 10). Отклоняясь в магнитном поле, электрон, спустя некоторое время, покинул соленоид. Определите время движения электрона внутри соленоида. 
.
, то
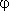можно найти из прямоугольного треугольника О1СО:
(5)
R2. Как видно из соотношения (5), заряд зависит от скорости движения пластины. Если пластина движется с ускорением, то скорость растет, и заряды на сторонах пластины будут меняться. Следовательно, в пластине возникнет ток. Сила тока будет равна
(6)
, в течение которых силу Ампера можно считать постоянной. Для каждого такого промежутка времени можно записать: 
- изменение импульса стержня за время 
(7)
- заряд, прошедший через поперечное сечение стержня за время 
(8)
где 
- плотность меди. Подставляя значение массы m в (8), получим: 
= 0,5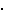
108 Кл/кг.
и 
. В те моменты, когда скорость частицы направлена противоположно 
= 0,1. Определите отношение E/Bv0.
